USACO 2018 Jan Solution
USACO 2018 Jan Solution更好的阅读体验戳此进入题面 Luogu 链接LG-P4188 [USACO18JAN]Lifeguards S题面SolutionCodeLG-P4182 [USACO18JAN]Lifeguards P题面ExamplesSolutionCodeLG-P4181 [USACO18JAN]Rental Service S题面ExamplesSolutionCodeLG-P6111 [USACO18JAN]MooTube S题面ExamplesSolutionCodeLG-P4185 [USACO18JAN]MooTube G题面ExamplesSolutionCodeLG-P4184 [USACO18JAN]Sprinklers P题面ExamplesSolutionCodeLG-P4187 [USACO18JAN]Stamp Painting G题面ExamplesSolutionCodeLG-P4186 [USACO18JAN]Cow at Large G题面ExamplesSolutionCodeLG-P4183 [USACO18JAN]Cow at Large P题面ExamplesSolutionCodeUPD
更好的阅读体验戳此进入
题面 Luogu 链接
LG-P4188 [USACO18JAN]Lifeguards S
题面
给定
Input_1
xxxxxxxxxx41325 931 443 7
Output_1
xxxxxxxxxx117
Solution
估计你们读完题之后也能想到线段树的做法,线段树做法十分显然,离散化之后建个权值线段树,然后所有线段插进去再每次删一个区间求
Code
xxxxxxxxxx721
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23template< typename T = int >24inline T read(void);25
26struct Line{27 int l, r;28 friend const bool operator < (const Line &a, const Line &b){return a.l < b.l;}29}a[110000];30vector < int > pos;31int N;32int d[210000];33int sum[210000];34
35int main(){36 N = read();37 for(int i = 1; i <= N; ++i)a[i].l = read(), a[i].r = read(), pos.emplace_back(a[i].l), pos.emplace_back(a[i].r);38 sort(pos.begin(), pos.end());39 auto endpos = unique(pos.begin(), pos.end());40 int siz = distance(pos.begin(), endpos);41 for(int i = 1; i <= N; ++i)42 a[i].l = distance(pos.begin(), upper_bound(pos.begin(), endpos, a[i].l)),43 a[i].r = distance(pos.begin(), upper_bound(pos.begin(), endpos, a[i].r));44 for(int i = 1; i <= N; ++i)d[a[i].l]++, d[a[i].r]--;45 int tot(0);46 for(int i = 1; i < siz; ++i){47 d[i] += d[i - 1];48 if(d[i])tot += pos.at(i + 1 - 1) - pos.at(i - 1);49 if(d[i] == 1)sum[i] += pos.at(i + 1 - 1) - pos.at(i - 1);50 sum[i] += sum[i - 1];51 }int mx(-1);52 for(int i = 1; i <= N; ++i)mx = max(mx, tot - (sum[a[i].r - 1] - sum[a[i].l - 1]));53 printf("%d\n", mx);54 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);55 return 0;56}57
58template < typename T >59inline T read(void){60 T ret(0);61 short flag(1);62 char c = getchar();63 while(c != '-' && !isdigit(c))c = getchar();64 if(c == '-')flag = -1, c = getchar();65 while(isdigit(c)){66 ret *= 10;67 ret += int(c - '0');68 c = getchar();69 }70 ret *= flag;71 return ret;72}LG-P4182 [USACO18JAN]Lifeguards P
题面
加强版来咯
给定
Examples
Input_1
xxxxxxxxxx413 221 837 1542 14
Output_1
xxxxxxxxxx1112
Solution
首先不难想到对于区间
然后 DP 显然,也很好想到一个状态
考虑优化,状态没什么可优化的,于是考虑优化转移,我们尝试提出来与转移时的
所以我们直接对前者维护一个最大值(因为我们的区间之间使有序的,所以如果对于之前的区间已经无交了,对于现在的一定也无交),后者则维护一个单调队列单调栈单调双端队列,每次处理时先把对应单调双端队列队头中所有不合法的,也就是不交的弹出然后更新不交区间里面的最大值。然后用交的和不交的里的最大值更新当前
如果你仔细想一下就会发现这个算法有一点问题,首先我们在最初的找单调双端队列里面的队头不合法的值的时候,我们时按照
这几个问题困扰了我很久,完全没有头绪,直到发现了一个性质我才大概能感性理解这个贪心的正确性。
显然当我们转移的时候,如果转移的这个
此时我们再回到刚才的考虑,我们的单调优先队列维护的是最大值,而最大值一定是
于是这个贪心(应该)是正确的。
当然上面这一大段证明都完全是我口糊的,不保证正确性,也不够理性和严谨,期待一个更严谨的证明。
Code
xxxxxxxxxx861
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23template< typename T = int >24inline T read(void);25
26struct Line{27 int l, r;28 friend const bool operator < (const Line &a, const Line &b){if(a.l == b.l)return a.r < b.r; return a.l < b.l;}29}line[110000];30list < Line > _line;31int N, K;32int cnt(0);33struct Status{int idx; int val;};34deque < Status > bst[110000];35int mx[110000];36int dp[110000][110];37
38int main(){39 N = read(), K = read();40 for(int i = 1; i <= N; ++i){41 int l = read(), r = read();42 _line.emplace_back(Line{l, r});43 }_line.sort();44 for(auto it = next(_line.begin()); it != _line.end();)45 if(it->r <= prev(it)->r)it = _line.erase(it), --K; else ++it;46 for(auto ln : _line)line[++cnt] = ln;47 N = cnt; K = max(0, K);48 for(int i = 1; i <= N; ++i){49 for(int k = 0; k <= min(i - 1, K); ++k){50 int xi = i - k - 1;51 while(!bst[xi].empty() && line[bst[xi].front().idx].r < line[i].l){52 auto tp = bst[xi].front(); bst[xi].pop_front();53 mx[xi] = max(mx[xi], tp.val + line[tp.idx].r);54 }55 dp[i][k] = max({56 dp[i][k],57 mx[xi] + line[i].r - line[i].l,58 bst[xi].empty() ? -1 : bst[xi].front().val + line[i].r59 });60 int val = dp[i][k] - line[i].r;61 int pos = i - k;62 while(!bst[pos].empty() && bst[pos].back().val < val)bst[pos].pop_back();63 bst[pos].push_back(Status{i, val});64 }65 }int ans(-1);66 for(int i = N - K; i <= N; ++i)ans = max(ans, dp[i][K - (N - i)]);67 printf("%d\n", ans);68 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);69 return 0;70}71
72template < typename T >73inline T read(void){74 T ret(0);75 short flag(1);76 char c = getchar();77 while(c != '-' && !isdigit(c))c = getchar();78 if(c == '-')flag = -1, c = getchar();79 while(isdigit(c)){80 ret *= 10;81 ret += int(c - '0');82 c = getchar();83 }84 ret *= flag;85 return ret;86}LG-P4181 [USACO18JAN]Rental Service S
题面
sssmzy 有
Examples
Input_1
xxxxxxxxxx1315 3 42632445761710 2582 10915 15102501180121001340
Output_1
xxxxxxxxxx11725
Solution
大水题,贪心 + 模拟,且贪心也很显然,只是写起来比较恶心,有语法题那味了,开始以为是我实现太差了,翻了一下题解区也都挺长。
显然几个贪心策略就是:
- 如果要卖彩虹犇,一定优先卖给
- 如果要卖彩虹糖,一定优先卖给
- 如果要保留彩虹犇,一定优先保留日产彩虹糖更多的犇。
然后就没啥可说的了,精细实现就可以了,有很多需要判断的地方比如
复杂度 long long。
Code
xxxxxxxxxx951
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23
25template< typename T = int >26inline T read(void);27
28int N, M, R;29int c[110000];30struct Milk{31 int pri, siz;32 friend const bool operator < (const Milk &a, const Milk &b){33 if(a.pri == b.pri)return a.siz > b.siz;34 return a.pri > b.pri;35 }36}mlk[110000];37int buy[110000];38int cur(0);39
40signed main(){41 N = read(), M = read(), R = read();42 for(int i = 1; i <= N; ++i)c[i] = read();43 for(int i = 1; i <= M; ++i)mlk[i].siz = read(), mlk[i].pri = read();44 for(int i = 1; i <= R; ++i)buy[i] = read();45 sort(c + 1, c + N + 1, greater < int >());46 sort(mlk + 1, mlk + M + 1);47 sort(buy + 1, buy + R + 1, greater < int >());48 int unsel(0), sel(N);49 int curus(0);50 int curs(N);51 int lftmlk(0);52 int curmlkn(0);53 int mx(-1);54 for(int i = 1; i <= min(N, R); ++i)cur += buy[i];55 do{56 while(curus < unsel)lftmlk += c[++curus];57 while(lftmlk && curmlkn < M){58 ++curmlkn;59 if(lftmlk >= mlk[curmlkn].siz)60 cur += mlk[curmlkn].siz * mlk[curmlkn].pri,61 lftmlk -= mlk[curmlkn].siz;62 else63 cur += lftmlk * mlk[curmlkn].pri,64 mlk[curmlkn].siz -= lftmlk,65 lftmlk = 0,66 --curmlkn;67 }68 while(curs > sel){69 if(curs <= R)cur -= buy[curs];70 --curs;71 }72 mx = max(mx, cur);73 // printf("sel:%lld, unsel:%lld, cur=%lld\n", sel, unsel, cur);74 --sel, ++unsel;75 }while(unsel <= N || sel >= 0);76 printf("%lld\n", mx);77 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);78 return 0;79}80
81template < typename T >82inline T read(void){83 T ret(0);84 short flag(1);85 char c = getchar();86 while(c != '-' && !isdigit(c))c = getchar();87 if(c == '-')flag = -1, c = getchar();88 while(isdigit(c)){89 ret *= 10;90 ret += int(c - '0');91 c = getchar();92 }93 ret *= flag;94 return ret;95}LG-P6111 [USACO18JAN]MooTube S
题面
给定
我知道你很急,但是你别急,我知道你有更优的方法,但是你别优,看看数据范围,想点普及难度的做法。
Examples
Input_1
xxxxxxxxxx714 321 2 332 3 242 4 451 264 173 1
Output_1
xxxxxxxxxx3132032
Solution
来个最无脑的做法,每个点开个 vector dfs 一遍维护到其它
Code
xxxxxxxxxx731
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23template< typename T = int >24inline T read(void);25
26struct Edge{27 Edge* nxt;28 int to;29 int val;30 OPNEW;31}ed[11000];32ROPNEW(ed);33Edge* head[5100];34vector < int > vert[5100];35int N, Q;36
37void dfs(int rt, int p, int fa = 0, int cur = 0){38 if(cur)vert[rt].emplace_back(cur);39 for(auto i = head[p]; i; i = i->nxt)40 if(SON != fa)dfs(rt, SON, p, cur ? min(cur, i->val) : i->val);41}42
43int main(){44 N = read(), Q = read();45 for(int i = 1; i <= N - 1; ++i){46 int s = read(), t = read(), val = read();47 head[s] = new Edge{head[s], t, val};48 head[t] = new Edge{head[t], s, val};49 }50 for(int i = 1; i <= N; ++i)dfs(i, i), sort(vert[i].begin(), vert[i].end());51 while(Q--){52 int dis = read(), p = read();53 printf("%d\n", (int)distance(lower_bound(vert[p].begin(), vert[p].end(), dis), vert[p].end()));54 }55 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);56 return 0;57}58
59template < typename T >60inline T read(void){61 T ret(0);62 short flag(1);63 char c = getchar();64 while(c != '-' && !isdigit(c))c = getchar();65 if(c == '-')flag = -1, c = getchar();66 while(isdigit(c)){67 ret *= 10;68 ret += int(c - '0');69 c = getchar();70 }71 ret *= flag;72 return ret;73}LG-P4185 [USACO18JAN]MooTube G
题面
题意与上一题不变,数据范围加大了。
给定
Examples
Input_1
xxxxxxxxxx714 321 2 332 3 242 4 451 264 173 1
Output_1
xxxxxxxxxx3132032
Solution
还是挺人类智慧的,全离线下来就行了。
不难想到对于
Code
xxxxxxxxxx871
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23template< typename T = int >24inline T read(void);25
26class UnionFind{27private:28 int siz[110000];29 int fa[110000];30public:31 UnionFind(void){for(int i = 1; i <= 101000; ++i)fa[i] = i, siz[i] = 1;}32 int Find(int x){return x == fa[x] ? x : fa[x] = Find(fa[x]);}33 void Union(int origin, int son){34 if(Find(origin) == Find(son))return;35 siz[Find(origin)] += siz[Find(son)];36 fa[Find(son)] = Find(origin);37 }38 int GetSiz(int x){return siz[Find(x)] - 1;}39}uf;40struct Edge{41 int s, t;42 int val;43 friend const bool operator < (const Edge &a, const Edge &b){return a.val < b.val;}44};std::priority_queue < Edge > ed;45int ans[110000];46struct Query{47 int v, k;48 int idx;49 friend const bool operator < (const Query &a, const Query &b){return a.k > b.k;}50}qs[110000];51int N, Q;52
53int main(){54 N = read(), Q = read();55 for(int i = 1; i <= N - 1; ++i){56 int s = read(), t = read(), val = read();57 ed.push(Edge{s, t, val});58 }59 for(int i = 1; i <= Q; ++i){60 int k = read(), v = read();61 qs[i] = Query{v, k, i};62 }sort(qs + 1, qs + Q + 1);63 for(int i = 1; i <= Q; ++i){64 while(!ed.empty() && ed.top().val >= qs[i].k)65 uf.Union(ed.top().s, ed.top().t), ed.pop();66 ans[qs[i].idx] = uf.GetSiz(qs[i].v);67 }68 for(int i = 1; i <= Q; ++i)printf("%d\n", ans[i]);69 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);70 return 0;71}72
73template < typename T >74inline T read(void){75 T ret(0);76 short flag(1);77 char c = getchar();78 while(c != '-' && !isdigit(c))c = getchar();79 if(c == '-')flag = -1, c = getchar();80 while(isdigit(c)){81 ret *= 10;82 ret += int(c - '0');83 c = getchar();84 }85 ret *= flag;86 return ret;87}LG-P4184 [USACO18JAN]Sprinklers P
题面
或者也可以描述为,给定
Examples
Input_1
xxxxxxxxxx61520 431 142 253 064 3
Output_1
xxxxxxxxxx1121
Solution
一道奇怪的题,最终可以转化为无脑推柿子。
首先借一个题解区的图:
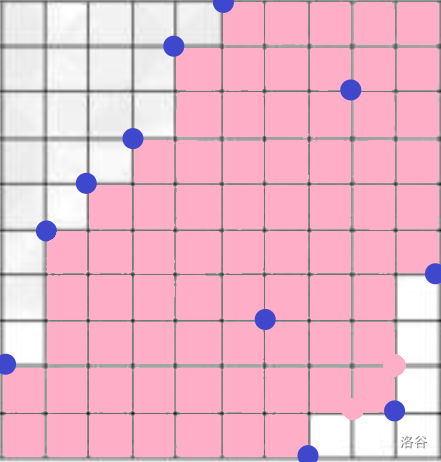
不难发现一个妙妙性质,即在第 点矩形的东西,然后化简。令
然后我们令
然后就成功从
Code
xxxxxxxxxx721
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23
27template< typename T = int >28inline T read(void);29
30int N;31int y[110000];32int l[110000], r[110000], up[110000];33ll sum1[110000];34ll sum2[110000];35
36int main(){37 N = read();38 for(int i = 1; i <= N; ++i){39 int rx = read() + 1, ry = read() + 1;40 y[rx] = ry;41 }l[0] = INT_MAX; r[N + 1] = -1;42 for(int i = 1; i <= N; ++i)l[i] = min(l[i - 1], y[i]);43 for(int i = N; i >= 1; --i)r[i] = max(r[i + 1], y[i]);44 int cur = r[1];45 for(int i = 1; i <= N; ++i)while(cur && cur >= l[i])up[cur] = i, --cur;46 for(int i = 1; i <= N; ++i)sum1[i] = (sum1[i - 1] + up[i]) % MOD;47 for(int i = 1; i <= N; ++i)sum2[i] = (sum2[i - 1] + sum1[i]) % MOD;48 ll ans(0);49 for(int i = 1; i <= N; ++i){50 ans = (ans + ((ll)r[i] - l[i]) * (r[i] - l[i] + 1) / 2ll % MOD * i % MOD) % MOD;51 ans = (ans - GetSum2(r[i] - 1) + GetSum2(l[i] - 2) + MOD) % MOD;52 ans = (ans + ((ll)r[i] - l[i] + 1) * GetSum1(l[i] - 1) % MOD) % MOD;53 }printf("%lld\n", ans);54 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);55 return 0;56}57
58template < typename T >59inline T read(void){60 T ret(0);61 short flag(1);62 char c = getchar();63 while(c != '-' && !isdigit(c))c = getchar();64 if(c == '-')flag = -1, c = getchar();65 while(isdigit(c)){66 ret *= 10;67 ret += int(c - '0');68 c = getchar();69 }70 ret *= flag;71 return ret;72}LG-P4187 [USACO18JAN]Stamp Painting G
题面
给定
Examples
Input_1
xxxxxxxxxx113 2 2
Output_1
xxxxxxxxxx116
Solution
我们发现这样涂的最终状态一定为至少有一段长度为
这真的是紫色的题吗。。
Code
xxxxxxxxxx651
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23
25template< typename T = int >26inline T read(void);27
28int N, M, K;29ll dp[1100000];30ll sum[1100000];31ll qpow(ll a, ll b){32 ll ret(1), mul(a);33 while(b){34 if(b & 1)ret = ret * mul % MOD;35 b >>= 1;36 mul = mul * mul % MOD;37 }return ret;38}39
40int main(){41 N = read(), M = read(), K = read();42 dp[0] = sum[0] = 1;43 for(int i = 1; i <= N; ++i)44 dp[i] = i < K ? dp[i - 1] * M % MOD : (sum[i - 1] - sum[i - K] + MOD) % MOD * (M - 1) % MOD,45 sum[i] = (sum[i - 1] + dp[i]) % MOD;46 printf("%lld\n", (qpow(M, N) - dp[N] + MOD) % MOD);47 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);48 return 0;49}50
51template < typename T >52inline T read(void){53 T ret(0);54 short flag(1);55 char c = getchar();56 while(c != '-' && !isdigit(c))c = getchar();57 if(c == '-')flag = -1, c = getchar();58 while(isdigit(c)){59 ret *= 10;60 ret += int(c - '0');61 c = getchar();62 }63 ret *= flag;64 return ret;65}LG-P4186 [USACO18JAN]Cow at Large G
题面
给定
Examples
Input_1
xxxxxxxxxx717 121 231 343 453 564 675 7
Output_1
xxxxxxxxxx113
Solution
考虑当 zpair 走到某个节点时,若有至少一只 sssmzy 距离该店的路程不大于 zpair,那么 zpair 走到此处时一定可以被截住并无法往下走,所以我们考虑尽可能早地堵死 zpair 的所有可能路径。
考虑 DFS 预处理每个点深度
Code
xxxxxxxxxx791
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23template< typename T = int >24inline T read(void);25
26int N, S;27int ans(0);28struct Edge{29 Edge* nxt;30 int to;31 OPNEW;32}ed[210000];33ROPNEW(ed);34Edge* head[110000];35
36int mn[110000];37int dep[110000];38int dfs_pre(int p = S, int fa = 0){39 dep[p] = dep[fa] + 1;40 if(!head[p]->nxt)mn[p] = dep[p];41 for(auto i = head[p]; i; i = i->nxt)42 if(SON != fa)43 mn[p] = min(mn[p], dfs_pre(SON, p));44 return mn[p];45}46void dfs(int p = S, int fa = 0){47 if(dep[p] > mn[p] - dep[p])return ++ans, void();48 for(auto i = head[p]; i; i = i->nxt)if(SON != fa)dfs(SON, p);49}50int main(){51 memset(mn, 0x3f, sizeof mn);52 N = read(), S = read();53 for(int i = 1; i <= N - 1; ++i){54 int s = read(), t = read();55 head[s] = new Edge{head[s], t};56 head[t] = new Edge{head[t], s};57 }if(!head[S]->nxt)printf("1\n"), exit(0);58 dfs_pre();59 dfs();60 printf("%d\n", ans);61 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);62 return 0;63}64
65template < typename T >66inline T read(void){67 T ret(0);68 short flag(1);69 char c = getchar();70 while(c != '-' && !isdigit(c))c = getchar();71 if(c == '-')flag = -1, c = getchar();72 while(isdigit(c)){73 ret *= 10;74 ret += int(c - '0');75 c = getchar();76 }77 ret *= flag;78 return ret;79}LG-P4183 [USACO18JAN]Cow at Large P
题面
加强版又来咯
给定
Examples
Input_1
xxxxxxxxxx71721 231 343 453 564 675 7
Output_1
xxxxxxxxxx713213343536171
Solution
好题,淀粉质。
首先延续一下上一题的结论,对于一个能堵住 sssmzy 的节点应该是符合
以上这些还都是比较好想的,后面就要开始人类智慧了。以上这个东西我们不可以想到,如果让符合条件的
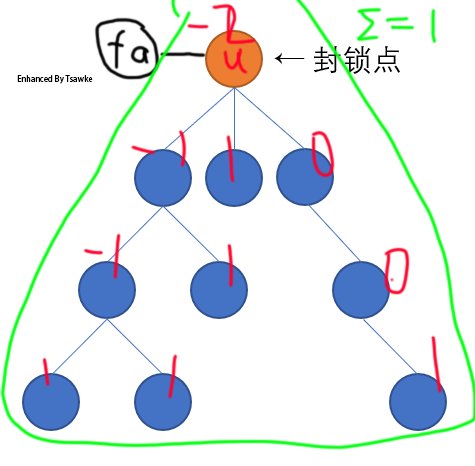
比如这个图,我们显然这个
然后我们发现这个 你们肯定都会。
Code
xxxxxxxxxx1411
4
11using namespace std;12using namespace __gnu_pbds;13
14mt19937 rnd(random_device{}());15int rndd(int l, int r){return rnd() % (r - l + 1) + l;}16bool rnddd(int x){return rndd(1, 100) <= x;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21typedef long double ld;22
23template< typename T = int >24inline T read(void);25
26int N;27struct Edge{28 Edge* nxt;29 int to;30 OPNEW;31}ed[210000];32ROPNEW(ed);33Edge* head[110000];34
35int ans[110000];36bool vis[110000];37int deg[110000], dep[110000], dleaf[110000];38
39void dfs_pre(int p = 1, int fa = 0){40 if(deg[p] == 1)dleaf[p] = 0;41 for(auto i = head[p]; i; i = i->nxt){42 if(SON == fa)continue;43 dfs_pre(SON, p);44 dleaf[p] = min(dleaf[p], dleaf[SON] + 1);45 }46}47void dfs_pre_from_root(int p = 1, int fa = 0){48 for(auto i = head[p]; i; i = i->nxt){49 if(SON == fa)continue;50 dleaf[SON] = min(dleaf[SON], dleaf[p] + 1);51 dfs_pre_from_root(SON, p);52 }53}54
55int mx[110000];56int siz[110000];57int rt(0);58void ResetRoot(void){rt = 0, mx[rt] = N;}59void dfs_rt(int p = 1, int fa = 0, int Siz = N){60 siz[p] = 1; mx[p] = 0;61 for(auto i = head[p]; i; i = i->nxt){62 if(SON == fa || vis[SON])continue;63 dfs_rt(SON, p, Siz);64 siz[p] += siz[SON];65 mx[p] = max(mx[p], siz[SON]);66 }mx[p] = max(mx[p], Siz - siz[p]);67 if(mx[p] < mx[rt])rt = p;68}69
70struct Status{71 int dep, val;72 friend const bool operator < (const Status &a, const Status &b){return a.dep < b.dep;}73}idx[110000], nod[110000];74int cnt(0);75void dfs_dep(int p, int fa, int cur = 0){76 dep[p] = cur;77 for(auto i = head[p]; i; i = i->nxt){78 if(SON == fa || vis[SON])continue;79 dfs_dep(SON, p, cur + 1);80 }81}82void dfs_upd(int p, int fa){83 idx[++cnt] = Status{dep[p], p},84 nod[cnt] = Status{dleaf[p] - dep[p], 2 - deg[p]};85 for(auto i = head[p]; i; i = i->nxt)if(SON != fa && !vis[SON])dfs_upd(SON, p);86}87
88void Cal(int p, int fa, int flag){89 cnt = 0;90 dfs_upd(p, fa);91 sort(idx + 1, idx + cnt + 1), sort(nod + 1, nod + cnt + 1);92 int sum(0), sp(0);93 for(int i = 1; i <= cnt; ++i){94 while(sp <= cnt - 1 && nod[sp + 1].dep <= idx[i].dep)sum += nod[++sp].val;95 ans[idx[i].val] += flag * sum;96 }97}98void Make(int p){99 vis[p] = true;100 dfs_dep(p, 0);101 Cal(p, 0, 1);102 for(auto i = head[p]; i; i = i->nxt){103 if(vis[SON])continue;104 Cal(SON, p, -1);105 ResetRoot();106 dfs_rt(SON, p, siz[SON]);107 Make(rt);108 }109}110
111int main(){112 // freopen("P4183_3.in", "r", stdin);113 N = read();114 for(int i = 1; i <= N - 1; ++i){115 int s = read(), t = read();116 head[s] = new Edge{head[s], t};117 head[t] = new Edge{head[t], s};118 ++deg[s], ++deg[t];119 }memset(dleaf, 0x3f, sizeof(dleaf));120 dfs_pre(); dfs_pre_from_root();121 ResetRoot(); dfs_rt(); /*dfs_rt(rt);*/ Make(rt);122 for(int i = 1; i <= N; ++i)printf("%d\n", deg[i] == 1 ? 1 : ans[i]);123 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);124 return 0;125}126
127template < typename T >128inline T read(void){129 T ret(0);130 short flag(1);131 char c = getchar();132 while(c != '-' && !isdigit(c))c = getchar();133 if(c == '-')flag = -1, c = getchar();134 while(isdigit(c)){135 ret *= 10;136 ret += int(c - '0');137 c = getchar();138 }139 ret *= flag;140 return ret;141}UPD
update-2022_11_07 初稿