Tsawke 的十二月模拟赛 题解

God does not play dice with the universe

原题是 LG-P3779 [SDOI2017] 龙与地下城。

关于自适应辛普森 Simpson - 辛普森法 学习笔记。

题面

给定一个 $m$$m$ 面的骰子，等概率产出 $0,1,2,\cdots ,m-1$$0, 1, 2, \cdots, m - 1$，投 $n$$n$ 次，求投出来的数之和在区间 $[A,B]$$[A, B]$ 的概率。

Solution

首先介绍一点前置知识：

正态分布：图形不再赘述，唯一需要注意的就是随机变量 $X$$X$ 的正态分布只需要它的期望 $\mu$$\mu$ 和方差 ${\sigma }^2$$\sigma^2$ 即可描述，记作 $N(\mu ,{\sigma }^2)$$N(\mu, \sigma^2)$，不难发现这恰好对应着题干。

概率密度函数：依然考虑一个随机变量 $X$$X$，若其为离散的那么显然可以简单的求出任意点的概率。但若其为连续型的，那么一个点的概率在极限意义下为 $0$$0$，然然而查询一段区间的时候显然不为 $0$$0$，所以我们便引入了概率密度函数来描述这个概率，对于随机变量 $X$$X$ 的概率密度函数 $f(x)$$f(x)$，需要满足 $f(x)$$f(x)$ 在区间内的积分等于 $X$$X$ 落在该区间的概率。

然后有个结论：正态分布的概率密度函数为：

关于这个东西的证明。。。完全不是人看的，似乎只能强行记下来这个公式。。。如果你一定要看一下证明，网上倒是也有一个 正态分布推导过程。

然后还有就是 C++ 库里自带了个 erf 和 erfc，大概求的是误差函数的积分和互补误差函数之类的，（我不会），有兴趣可以看看。

然后所以如果我们能够证明本题这玩意是正态分布的，那么就直接对这个 $f(x)$$f(x)$ 做自适应辛普森，求一下积分就行了。

独立同分布：首先独立比较好理解，就是两个随机变量之间无影响，和高中数学里面的独立事件差不多。然后同分布就是指一些随机变量服从相同的分布。

Tips：概率论中 $E(X)$$E(X)$ 表示期望，$D(X)$$D(X)$ 表示方差。

中心极限定理：对于 $n$$n$ 个独立同分布（如本题中的相同骰子）的随机变量 $X_1,X_2,\cdots ,X_n$$X_1, X_2, \cdots, X_n$，若 $E(X_i)=\mu ,D(X_i)={\sigma }^2$$E(X_i) = \mu, D(X_i) = \sigma^2$，令：

若 $n$$n$ 足够大，则我们认为 $Y_n\sim N(0,1)$$Y_n \sim N(0, 1)$。

然后还有一个常用推论，当然首先我们需要知道正态分布的一点运算规则，即：

若 $X\sim N(a,b)$$X \sim N(a, b)$ 则 $cX\sim N(ca,c^{2}b)$$cX \sim N(ca, c^2b)$，从期望和方差的意义不难理解。

若 $X\sim N(a,b)$$X \sim N(a, b)$ 则 $X+c\sim N(a+c,b)$$X + c \sim N(a + c, b)$，同理不难得出。

所以我们可以将刚才的中心极限定理式子转化为：

也就是说，本题里求的这些骰子的点数和，实际上就是 $n$$n$ 个独立同分布的和，所以一定服从 $N(n\mu ,n{\sigma }^2)$$N(n\mu, n\sigma^2)$，用我们刚才写的正态分布概率密度函数带进去这个期望和方差然后求个积分即可。

然后发现这东西套个自适应辛普森就可以在 $O(\mathtt{\text{玄学}})$$O(\texttt{玄学})$ 的复杂度完成。

但是我们不难发现这个东西还有点问题，就是中心极限定理需要一个前提，$n$$n$ 足够大，对于一些 $n=1$$n = 1$ 之类的数据点用这个就显然寄了，所以我们要考虑一些数据点分治的做法。

显然对于 $n$$n$ 较小的数据，我们可以考虑多项式，多项式 $i$$i$ 次方项的系数为骰子值为 $i$$i$ 的概率，显然当 $n=1$$n = 1$ 时，假设骰子面数为 $m$$m$，不难想到多项式为 ${\displaystyle \frac{1}{m}}{x}^{m-1}+{\displaystyle \frac{1}{m}}{x}^{m-2}+\cdots +{\displaystyle \frac{1}{m}}{x}^1+{\displaystyle \frac{1}{m}}{x}^0$$\dfrac{1}{m}x^{m - 1} + \dfrac{1}{m}x^{m - 2} + \cdots + \dfrac{1}{m}x^1 + \dfrac{1}{m}x^0$。然后很容易想到对于其它的 $n$$n$ 结果就是这个多项式的 $n$$n$ 次方，我们只需要用 FFT 优化一下然后在结果里求出指数在 $[A,B]$$[A, B]$ 之间的系数和即可，这东西可以用多项式快速幂优化（这个实际上不算是多项式快速幂，因为最终多项式总长度较小，所以在正常 FFT 时写个复数的快速幂就行），我们可以分析一下，显然多项式初始项数最多为 $m$$m$，所以时间复杂度大概是 $O(nm\log nm)$$O(nm \log nm)$，常数不小，然后 $nm$$nm$ 是 $4e6$$4e6$ 级别的，总之 $nm\le 1e5$$nm \le 1e5$ 应该不成问题，而且因为我们的中心极限定理一般要求 $n\ge 30$$n \ge 30$ 就可以了，所以这个理论上就可以过了。

Tips：仅用多项式快速幂期望得分 60~70。

upd：上述过程就可以通过本题了，需要注意的一个问题是不要忘记在自适应辛普森的过程中限制层数，后文是我最开始写这道题时的因为没有限制层数的一些误区与另一种类似的方法，仅供参考。

如果不在自适应辛普森中限制层数，那么会有精度问题，原因除此之外还可能因拟合 $N(0,1)$$N(0, 1)$ 的概率密度函数会比拟合 $N(n\mu ,n{\sigma }^2)$$N(n\mu, n\sigma^2)$ 精度更高一点，可能因为 $n\mu$$n\mu$ 和 $n{\sigma }^2$$n\sigma^2$ 的值域范围太大了，再加上自适应辛普森本来精度就很玄学，所以会导致最终答案精度爆炸。

总之还可以考虑另一个方法，即中心极限定理的初始式子：

不难发现我们知道了限定的 $\sum _{i=1}^n{X}_i$$\sum_{i = 1}^n X_i$ 的范围，也就可以带进式子里直接推出 $Y_n$$Y_n$ 的范围，然后用自适应辛普森跑一下 $N(0,1)$$N(0, 1)$ 的概率密度函数，因为 $Y_n\sim N(0,1)$$Y_n \sim N(0, 1)$，所以求出对应范围之后直接求 $N(0,1)$$N(0, 1)$ 的概率密度函数在新范围里的积分即为答案。不过这样会发现依然是错误的如果在自适应辛普森中限制层数那么就没有问题了。

检查发现，对于正态分布中，在角落可能很小，从而导致 $[l,mid],[mid,r],[l,r]$$[l, mid], [mid, r], [l, r]$ 都很小，从而直接返回 $0$$0$，可以感性理解一下，所以可能会导致拟合的误差过大，于是考虑每次求范围 $[A,B]$$[A, B]$ 的时候分别拟合 $[0,A]$$[0, A]$ 和 $[0,B]$$[0, B]$，然后用 $[0,B]$$[0, B]$ 的值减去 $[0,A]$$[0, A]$ 的，这样是等效的，且会更多的引入较大的值使得精度更高，改成此方法后即使不限制层数也可以通过本题。

Tips：代码中注释部分即为后半部分的实现方式。

Code

x
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define SON i->to
8
#define OPNEW void* operator new(size_t)
9
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
10

11
using namespace std;
12

13
mt19937 rnd(random_device{}());
14
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
15
bool rnddd(int x){return rndd(1, 100) <= x;}
16

17
typedef unsigned int uint;
18
typedef unsigned long long unll;
19
typedef long long ll;
20
typedef long double ld;
21

22
#define comp complex < ld >
23
#define DFT (true)
24
#define IDFT (false)
25
#define EPS (ld)(1e-10)
26

27
template < typename T = int >
28
inline T read(void);
29

30
int N, M;
31

32
comp comp_qpow(comp a, ll b){
33
    comp ret(1.0, 0.0), mul(a);
34
    while(b){
35
        if(b & 1)ret = ret * mul;
36
        b >>= 1;
37
        mul = mul * mul;
38
    }return ret;
39
}
40

41
class Polynomial{
42
private:
43
public:
44
    int len;
45
    comp A[2100000];
46
    comp Omega(int n, int k, bool pat){
47
        if(pat == DFT)return comp(cos(2 * PI * k / n), sin(2 * PI * k / n));
48
        return conj(comp(cos(2 * PI * k / n), sin(2 * PI * k / n)));
49
    }
50
    void Reverse(comp* pol){
51
        int pos[len + 10];
52
        memset(pos, 0, sizeof pos);
53
        for(int i = 0; i < len; ++i){
54
            pos[i] = pos[i >> 1] >> 1;
55
            if(i & 1)pos[i] |= len >> 1;
56
        }
57
        for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
58
    }
59
    void FFT(comp* pol, int len, bool pat){
60
        Reverse(pol);
61
        for(int siz = 2; siz <= len; siz <<= 1)
62
            for(comp* p = pol; p != pol + len; p += siz){
63
                int mid = siz >> 1;
64
                for(int i = 0; i < mid; ++i){
65
                    auto tmp = Omega(siz, i, pat) * p[i + mid];
66
                    p[i + mid] = p[i] - tmp, p[i] = p[i] + tmp;
67
                }
68
            }
69
        if(pat == IDFT)
70
            for(int i = 0; i <= len; ++i)
71
            A[i].real(A[i].real() / (ld)len), A[i].imag(A[i].imag() / (ld)len);
72
    }
73
    void MakeFFT(void){
74
        FFT(A, len, DFT);
75
        for(int i = 0; i < len; ++i)A[i] = comp_qpow(A[i], N);
76
        FFT(A, len, IDFT);
77
    }
78
}poly;
79

80
ld mu, sigma2;
81

82
ld f(ld x){
83
    return exp(-(x - mu) * (x - mu) / 2.0 / sigma2) / sqrt(2.0 * PI * sigma2);
84
}
85
ld Simpson(ld a, ld b){
86
    return (b - a) * (f(a) + f(b) + 4 * f((a + b) / 2.0)) / 6.0;
87
}
88
ld Adaptive(ld l, ld r, ld cur, ld eps = 1e-6, ll dep = 1){
89
    ld mid = (l + r) / 2.0;
90
    ld lval = Simpson(l, mid), rval = Simpson(mid, r);
91
    if(dep >= 10 && fabs(lval + rval - cur) <= eps * 15.0)return lval + rval + (lval + rval - cur) / 15.0;
92
    return Adaptive(l, mid, lval, eps / 2.0, dep + 1) + Adaptive(mid, r, rval, eps / 2.0, dep + 1);
93
}
94

95
int main(){
96
    int T = read();
97
    while(T--){
98
        M = read(), N = read();
99
        if(N * M <= (int)1e5){
100
            memset(poly.A, 0, sizeof poly.A);
101
            for(int i = 0; i <= M - 1; ++i)
102
                poly.A[i].real((ld)1.0 / (ld)M), poly.A[i].imag(0.0);
103
            poly.len = 1;
104
            while(poly.len <= N * M)poly.len <<= 1;
105
            poly.MakeFFT();
106
            for(int i = 1; i <= 10; ++i){
107
                int A = read(), B = read();
108
                ld ans(0.0);
109
                for(int j = A; j <= B; ++j)ans += poly.A[j].real();
110
                printf("%.10Lf\n", ans);
111
            }
112
        }else{
113
            // mu = 0.0, sigma2 = 1.0;
114
            // ld real_mu = (ld)(M - 1) / 2.0;
115
            // ld real_sig = ((ld)M * M - 1.0) / 12.0;
116
            // for(int i = 1; i <= 10; ++i){
117
            //     int A = read(), B = read();
118
            //     ld L = (ld)((ld)A - N * real_mu) / sqrt(N * real_sig);
119
            //     ld R = (ld)((ld)B - N * real_mu) / sqrt(N * real_sig);
120
            //     printf("%.8Lf\n", Adaptive((ld)L, (ld)R, Simpson(L, R)));
121
            //     // printf("%.8Lf\n", Adaptive((ld)0, (ld)R, Simpson(0, R)) - Adaptive((ld)0, (ld)L, Simpson(0, L)));
122
            // }
123

124
            mu = (ld)N * (ld)(M - 1) / 2.0;
125
            sigma2 = (ld)N * (ld)((ll)M * M - 1) / 12.0;
126
            for(int i = 1; i <= 10; ++i){
127
                int A = read(), B = read();
128
                printf("%.8Lf\n", Adaptive((ld)A, (ld)B, Simpson(A, B)));
129
            }
130
        }
131
    }
132
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
133
    return 0;
134
}
135

136
template < typename T >
137
inline T read(void){
138
    T ret(0);
139
    int flag(1);
140
    char c = getchar();
141
    while(c != '-' && !isdigit(c))c = getchar();
142
    if(c == '-')flag = -1, c = getchar();
143
    while(isdigit(c)){
144
        ret *= 10;
145
        ret += int(c - '0');
146
        c = getchar();
147
    }
148
    ret *= flag;
149
    return ret;
150
}

真正的OIer从不女装

原题 LG-P5500 [LnOI2019]真正的OIer从不女装

显然一次反转和多次反转等效，即对应题目背景。同时亦等效为将查询区间的某个前缀拼在其最后，换句话说每一次反转操作代表着转换为任意一个循环同构的序列，同时这也印证了一次反转与多次反转等效。所以线段树维护区间最长相同子串，左端点的子串，右端点的子串，左右端点颜色，区间长度等，支持区间修改区间查询和初始化，然后询问的时候判一下 $k$$k$ 是不是 $0$$0$ 即可，随便写写就过了，很好写很好调。

xxxxxxxxxx
129
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define SON i->to
8
#define OPNEW void* operator new(size_t)
9
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
10

11
using namespace std;
12

13
mt19937 rnd(random_device{}());
14
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
15
bool rnddd(int x){return rndd(1, 100) <= x;}
16

17
typedef unsigned int uint;
18
typedef unsigned long long unll;
19
typedef long long ll;
20
typedef long double ld;
21

22
#define MAXN (210000)
23

24
template< typename T = int >
25
inline T read(void);
26

27
int N, M;
28
int a[MAXN];
29

30
struct Node{
31
    int mx;
32
    int mxl, mxr;
33
    int corl, corr;
34
    int siz;
35
    friend const Node operator + (const Node &l, const Node &r){
36
        Node ret;
37
        ret.mx = max({l.mx, r.mx, l.corr == r.corl ? l.mxr + r.mxl : 0});
38
        ret.mxl = max({l.mxl, l.mxl == l.siz && l.corr == r.corl ? l.mxl + r.mxl : 0});
39
        ret.mxr = max({r.mxr, r.mxr == r.siz && r.corl == l.corr ? r.mxr + l.mxr : 0});
40
        ret.corl = l.corl, ret.corr = r.corr;
41
        ret.siz = l.siz + r.siz;
42
        return ret;
43
    }
44
};
45

46
class SegTree{
47
private:
48
    Node tr[MAXN << 2];
49
    int lz[MAXN << 2];
50
    #define LS (p << 1)
51
    #define RS (LS | 1)
52
    #define MID ((gl + gr) >> 1)
53
    #define SIZ(l, r) (r - l + 1)
54
public:
55
    void Pushup(int p, int gl, int gr){tr[p] = tr[LS] + tr[RS];}
56
    void Pushdown(int p){
57
        tr[LS].mx = tr[LS].mxl = tr[LS].mxr = tr[LS].siz;
58
        tr[RS].mx = tr[RS].mxl = tr[RS].mxr = tr[RS].siz;
59
        tr[LS].corl = tr[LS].corr = lz[p];
60
        tr[RS].corl = tr[RS].corr = lz[p];
61
        lz[LS] = lz[RS] = lz[p];
62
        lz[p] = false;
63
    }
64
    void Build(int p = 1, int gl = 1, int gr = N){
65
        if(gl == gr)return tr[p].mx = tr[p].mxl = tr[p].mxr = tr[p].siz = 1, tr[p].corl = tr[p].corr = a[gl = gr], void();
66
        Build(LS, gl, MID), Build(RS, MID + 1, gr);
67
        Pushup(p, gl, gr);
68
    }
69
    void Assign(int l, int r, int v, int p = 1, int gl = 1, int gr = N){
70
        if(l <= gl && gr <= r){
71
            tr[p].mx = tr[p].mxl = tr[p].mxr = tr[p].siz;
72
            tr[p].corl = tr[p].corr = v;
73
            if(lz[p])Pushdown(p);
74
            lz[p] = v;
75
            return;
76
        }
77
        if(lz[p])Pushdown(p);
78
        if(l <= MID)Assign(l, r, v, LS, gl, MID);
79
        if(MID + 1 <= r)Assign(l, r, v, RS, MID + 1, gr);
80
        Pushup(p, gl, gr);
81
    }
82
    Node Query(int l, int r, int p = 1, int gl = 1, int gr = N){
83
        if(l <= gl && gr <= r)return tr[p];
84
        if(lz[p])Pushdown(p);
85
        return
86
            l <= MID && r >= MID + 1
87
                ? Query(l, r, LS, gl, MID) + Query(l, r, RS, MID + 1, gr)
88
                :(
89
                    l <= MID
90
                        ? Query(l, r, LS, gl, MID)
91
                        : Query(l, r, RS, MID + 1, gr)
92
                );
93
    }
94
}st;
95

96
int main(){
97
    N = read(), M = read();
98
    for(int i = 1; i <= N; ++i)a[i] = read();
99
    st.Build();
100
    while(M--){
101
        char c = getchar(); while(c != 'Q' && c != 'R')c = getchar();
102
        if(c == 'R'){
103
            int l = read(), r = read(), v = read();
104
            st.Assign(l, r, v);
105
        }else{
106
            int l = read(), r = read(), k = read();
107
            auto ans = st.Query(l, r);
108
            printf("%d\n", k && ans.corl == ans.corr ? max(min(ans.siz, ans.mxl + ans.mxr), ans.mx) : ans.mx);
109
        }
110
    }
111
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
112
    return 0;
113
}
114

115
template < typename T >
116
inline T read(void){
117
    T ret(0);
118
    int flag(1);
119
    char c = getchar();
120
    while(c != '-' && !isdigit(c))c = getchar();
121
    if(c == '-')flag = -1, c = getchar();
122
    while(isdigit(c)){
123
        ret *= 10;
124
        ret += int(c - '0');
125
        c = getchar();
126
    }
127
    ret *= flag;
128
    return ret;
129
}

简单数据结构

原题 LG-P5350 序列。

emm 感觉没什么好说的，就是无脑写个 ODT 即可，唯一需要注意的就是维护 ODT 的时候需要注意尽量保证序列里元素连续，也就是复制的时候先复制再删除，否则会有奇怪的未知错误。

然后如果你非要写可持久化平衡树我也不拦你。

xxxxxxxxxx
132
1
#define _USE_MATH_DEFINES
2
#include <bits/extc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define SON i->to
8
#define OPNEW void* operator new(size_t)
9
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
10

11
using namespace std;
12
using namespace __gnu_pbds;
13

14
mt19937 rnd(random_device{}());
15
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
16
bool rnddd(int x){return rndd(1, 100) <= x;}
17

18
typedef unsigned int uint;
19
typedef unsigned long long unll;
20
typedef long long ll;
21
typedef long double ld;
22

23
#define MOD (ll)(1e9 + 7)
24

25
template< typename T = int >
26
inline T read(void);
27

28
int N, M;
29
ll ans[310000];
30

31
struct Node{
32
    int l, r;
33
    mutable ll val;
34
    friend const bool operator < (const Node &a, const Node &b){return a.l < b.l;}
35
};
36
class ODT{
37
private:
38
    #define SIZ(it) (it->r - it->l + 1)
39
    set < Node > tr;
40
public:
41
    auto Insert(Node x){return tr.insert(x);}
42
    auto Split(int p){
43
        auto it = tr.lower_bound(Node{p});
44
        if(it != tr.end() && it->l == p)return it;
45
        --it;
46
        int l = it->l, r = it->r;
47
        ll v = it->val;
48
        tr.erase(it);
49
        Insert(Node{l, p - 1, v});
50
        return Insert(Node{p, r, v}).first;
51
    }
52
    void Assign(int l, int r, ll val){
53
        auto itR = Split(r + 1), itL = Split(l);
54
        tr.erase(itL, itR);
55
        Insert(Node{l, r, val});
56
    }
57
    void Modify(int l, int r, ll val){
58
        auto itR = Split(r + 1), itL = Split(l);
59
        for(auto it = itL; it != itR; ++it)it->val = (it->val + val) % MOD;
60
    }
61
    ll Query(int l, int r){
62
        ll ret(0);
63
        auto itR = Split(r + 1), itL = Split(l);
64
        for(auto it = itL; it != itR; ++it)ret = (ret + SIZ(it) * it->val % MOD) % MOD;
65
        return ret;
66
    }
67
    void Copy(int l1, int r1, int l2, int r2){
68
        auto itR = Split(r1 + 1), itL = Split(l1);
69
        basic_string < Node > tmp;
70
        for(auto it = itL; it != itR; ++it)tmp += Node{it->l + (l2 - l1), it->r + (l2 - l1), it->val};
71
        itR = Split(r2 + 1), itL = Split(l2);
72
        tr.erase(itL, itR);
73
        for(auto nod : tmp)Insert(nod);
74
    }
75
    void Swap(int l1, int r1, int l2, int r2){
76
        basic_string < Node > S, T;
77
        auto itR = Split(r1 + 1), itL = Split(l1);
78
        for(auto it = itL; it != itR; ++it)S += Node{it->l + (l2 - l1), it->r + (l2 - l1), it->val};
79
        tr.erase(itL, itR);
80
        itR = Split(r2 + 1), itL = Split(l2);
81
        for(auto it = itL; it != itR; ++it)T += Node{it->l - (l2 - l1), it->r - (l2 - l1), it->val};
82
        tr.erase(itL, itR);
83
        for(auto nod : S + T)Insert(nod);
84
    }
85
    void Reverse(int l, int r){
86
        basic_string < Node > vals;
87
        auto itR = Split(r + 1), itL = Split(l);
88
        for(auto it = itL; it != itR; ++it)vals += *it;
89
        tr.erase(itL, itR);
90
        for(auto nod : vals)Insert(Node{r - nod.r + l, r - nod.l + l, nod.val});
91
    }
92
    void SetAns(void){
93
        for(auto nod : tr)
94
            for(int i = nod.l; i <= nod.r; ++i)ans[i] = nod.val;
95
    }
96
}odt;
97

98
int main(){
99
    N = read(), M = read();
100
    for(int i = 1; i <= N; ++i)odt.Insert(Node{i, i, read()});
101
    while(M--){
102
        int opt = read();
103
        switch(opt){
104
            case 1:{int l = read(), r = read(); printf("%lld\n", odt.Query(l, r)); break;}
105
            case 2:{int l = read(), r = read(), val = read(); odt.Assign(l, r, val); break;}
106
            case 3:{int l = read(), r = read(), val = read(); odt.Modify(l, r, val); break;}
107
            case 4:{int l1 = read(), r1 = read(), l2 = read(), r2 = read(); odt.Copy(l1, r1, l2, r2); break;}
108
            case 5:{int l1 = read(), r1 = read(), l2 = read(), r2 = read(); odt.Swap(min(l1, l2), min(r1, r2), max(l1, l2), max(r1, r2)); break;}
109
            case 6:{int l = read(), r = read(); odt.Reverse(l, r); break;}
110
        }
111
    }
112
    odt.SetAns();
113
    for(int i = 1; i <= N; ++i)printf("%lld%c", ans[i], i == N ? '\n' : ' ');
114
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
115
    return 0;
116
}
117

118
template < typename T >
119
inline T read(void){
120
    T ret(0);
121
    int flag(1);
122
    char c = getchar();
123
    while(c != '-' && !isdigit(c))c = getchar();
124
    if(c == '-')flag = -1, c = getchar();
125
    while(isdigit(c)){
126
        ret *= 10;
127
        ret += int(c - '0');
128
        c = getchar();
129
    }
130
    ret *= flag;
131
    return ret;
132
}

什么？？？NP问题？？？

原题 LG-P4727 [HNOI2009]图的同构计数。

题解在这里有 Group Theory - 浅析群论。

首先称两个图同构，当且仅当两个图可以通过对顶点的重标号使得两图完全相同。

然后这个东西的答案是一个数列，OEIS 上的编号是 A000088。

然后我们再次回到 Burnside定理，集合 $X$$X$ 即为 $n$$n$ 个顶点可能构成的 $2^{(\genfrac{}{}{0ex}{}{n}{2})}=2^{\frac{n(n-1)}{2}}$$2^{n \choose 2} = 2^\tfrac{n(n - 1)}{2}$ 个简单无向图。置换群 $\mathbb{G}$$\mathbb{G}$ 即为 $[1,n]$$[1, n]$ 的全排列。

然后我们的难点依然在于求不动点的数量。也就是说对于一个置换 $g$$g$，有多少图在经过置换 $g$$g$ 之后与原图同构。

下面将会有一个与上一题，即 Polya定理 模板，或者说群论的标准套路。我们可以考虑先将图认为是完全图，然后用两种颜色对边进行染色，两种颜色表示该边存在或不存在。于是此时我们就会发现对于某一个置换 $g$$g$，仍然存在一个等价类中，所有边必须均存在或不存在。

举个例子，对于一个标号为 $1,2,3$$1, 2, 3$ 的三角形完全图，如果有置换 $g=(2,3,1)$$g = (2, 3, 1)$，那么此时不难发现三条边同属一个等价类，因为你要么使三条边均存在，要么均不存在，否则按照这个置换的意义，旋转一下三角形，就会使得图不同构。此时的 $g$$g$ 对应的不动点即为 $2^1=2$$2^1 = 2$ 个。

所以说上面我们说的这一对，就是标准的 Polya定理，即 $|X^g|=2^{c(g)}$$\lvert X^g \rvert = 2^{c(g)}$。

所以现在关键就在于我们如何求这个 $c(g)$$c(g)$。

首先我们会发现，对于一个置换 $g$$g$，其是可以被分成多个不相交的部分的，用双行表示法举个例子：

考虑若将置换 $g$$g$ 拆成 $k$$k$ 个循环，长度分别为 $b_1,b_2,\cdots ,b_k$$b_1, b_2, \cdots, b_k$。然后不难发现有两种边：

首先考虑对于两个点均在同一段循环内的边：

然后我们考虑对于一种置换中的一个长度为 $b$$b$ 的循环，有一个结论，这样的循环共有 $\lfloor {\displaystyle \frac{b}{2}}\rfloor$$\lfloor \dfrac{b}{2} \rfloor$ 个等价类。

我们可以将对应的点数排成一个正 $n$$n$ 边形，比如 $n=6$$n = 6$ 的时候，如果有这样一个置换 $\begin{array}{c}g=\left(\begin{array}{cccccc}1& 2& 3& 4& 5& 6\\ 2& 3& 4& 5& 6& 1\end{array}\right)\end{array}$$g = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 2 & 3 & 4 & 5 & 6 & 1 \end{pmatrix}$，存在这样的图和边：

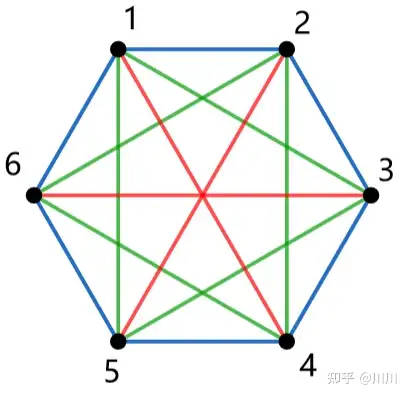
不难发现对于长度相同的边都是等价的，其必须同时染或不染，否则置换后将会不同构。而不难想到，由于正 $b$$b$ 边形存在对称性，所以线段的长度共有 $\lfloor {\displaystyle \frac{b}{2}}\rfloor$$\lfloor \dfrac{b}{2} \rfloor$ 种，所以等价类也就共有这些种。

于是其贡献的等价类数量为：$\sum _{i=1}^k\lfloor {\displaystyle \frac{b_i}{2}}\rfloor$$\sum_{i = 1}^k \lfloor \dfrac{b_i}{2} \rfloor$。

然后考虑在不同循环中的边：

举个例子：

这个东西的图大概是这样的：

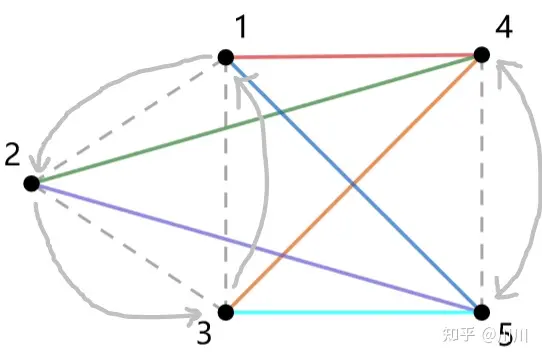
如对于长度为 $b_1,b_2$$b_1, b_2$ 的两个循环，那么两者之间共有 $b_1\times b_2$$b_1 \times b_2$ 条边，所以在这两者之间的边，每次经过 $\mathrm{lcm}(b_1,b_2)$$\operatorname{lcm}(b_1, b_2)$ 次置换之后就会回到原位，则等价类的大小，或者说环长为 $\mathrm{lcm}(b_1,b_2)$$\operatorname{lcm}(b_1, b_2)$，那么此时等价类个数，也就是环种类数，即为 ${\displaystyle \frac{b_1\times b_2}{\mathrm{lcm}(b_1,b_2)}}$$\dfrac{b_1 \times b_2}{\operatorname{lcm}(b_1, b_2)}$，也就是 $gcd(b_1,b_2)$$\gcd(b_1, b_2)$。

所以这些边的贡献的等价类个数即为：

所以最终等价类的个数即为：

答案即为：

不过 $\mathbb{G}$$\mathbb{G}$ 是 $n!$$n!$ 的，复杂度肯定不行，尝试优化；

考虑发现很多置换会被重复计算，如：

这样的 $b_k$$b_k$ 都是 $1,2,3$$1, 2, 3$，那么 $c(g)$$c(g)$ 的值是相同的。

也就是说对于相同的 $n$$n$ 的拆分贡献是相同的，所以可以考虑枚举 $n$$n$ 的拆分。

考虑对于一种拆分，计算有多少种对应的置换，首先总共有 $n!$$n!$，但是对于每一段长度为 $b$$b$ 的循环，都需要使其从普通排列转换为圆排列，也就是先去掉重复的 $b!$$b!$，然后再乘上圆排列的 $(b-1)!$$(b - 1)!$，并且对于相同长度的多个循环，假设有 $c$$c$ 个，那么这里又会重复 $c!$$c!$ 个，那么在去重后应该为：

然后这里再枚举每个 $n$$n$ 的拆分，答案即为：

然后化简一下即为：

这样便可以通过了。然后尝试分析一下复杂度：

枚举 $n$$n$ 的拆分是 A000041，然后对于拆分长度为 $k$$k$ 的求解为 $O(k^2)$$O(k^2)$ 的，最终应为 A296010，然后这个东西完全不知道怎么分析，总之最后的复杂度大约在 $O({10}^{\sqrt{n}})$$O(10^{\sqrt{n}})$，虽然我也不知道是怎么分析出来的。。。

xxxxxxxxxx
95
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define SON i->to
8
#define OPNEW void* operator new(size_t)
9
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
10

11
using namespace std;
12

13
mt19937 rnd(random_device{}());
14
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
15
bool rnddd(int x){return rndd(1, 100) <= x;}
16

17
typedef unsigned int uint;
18
typedef unsigned long long unll;
19
typedef long long ll;
20
typedef long double ld;
21

22
#define MOD (997)
23

24
template < typename T = int >
25
inline T read(void);
26

27
int N;
28
ll fact[110], inv[110], inv_d[110];
29
int cnt[110];
30
ll ans(0);
31
basic_string < int > cur;
32
unordered_set < int > exist;
33

34
ll qpow(ll a, ll b){
35
    ll ret(1), mul(a);
36
    while(b){
37
        if(b & 1)ret = ret * mul % MOD;
38
        b >>= 1;
39
        mul = mul * mul % MOD;
40
    }return ret;
41
}
42

43
void Init(void){
44
    for(int i = 1; i <= 100; ++i)inv_d[i] = qpow(i, MOD - 2);
45
    fact[0] = 1;
46
    for(int i = 1; i <= 100; ++i)fact[i] = fact[i - 1] * i % MOD;
47
    inv[100] = qpow(fact[100], MOD - 2);
48
    for(int i = 99; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
49
}
50

51
void dfs(int lft = N){
52
    if(!lft){
53
        ll C(0);
54
        for(auto i : cur)C += i >> 1;
55
        for(int i = 1; i <= (int)cur.size(); ++i)
56
            for(int j = 1; j <= i - 1; ++j)
57
                C += __gcd(cur.at(i - 1), cur.at(j - 1));
58
        ll ret = qpow(2, C);
59
        for(auto i : cur)(ret *= inv_d[i]) %= MOD;
60
        for(auto i : exist)(ret *= inv[cnt[i]]) %= MOD;
61
        (ans += ret) %= MOD;
62
        return;
63
    }
64
    for(int i = cur.empty() ? 1 : cur.back(); i <= lft; ++i){
65
        cur += i, ++cnt[i], exist.insert(i);
66
        dfs(lft - i);
67
        cur.pop_back();
68
        if(!--cnt[i])exist.erase(i);
69
    }
70
}
71

72
int main(){
73
    Init();
74
    N = read();
75
    dfs();
76
    printf("%lld\n", ans);
77
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
78
    return 0;
79
}
80

81
template < typename T >
82
inline T read(void){
83
    T ret(0);
84
    int flag(1);
85
    char c = getchar();
86
    while(c != '-' && !isdigit(c))c = getchar();
87
    if(c == '-')flag = -1, c = getchar();
88
    while(isdigit(c)){
89
        ret *= 10;
90
        ret += int(c - '0');
91
        c = getchar();
92
    }
93
    ret *= flag;
94
    return ret;
95
}