题面

$n \times n$ $n$ $(0, 0)$ $(n - 1, n - 1)$ $n$ $(i, j)$ $\forall(x, y), x \in [i, n - 1], y \in [j, n - 1]$ $\forall(x, y), x \in [0, i], y \in [0, j]$ 进行施肥，要求选出一片矩形，使得其中每个格点都既浇水又施肥，求方案数。

$n$ 个关键点，要求选一个矩形使得其中左上右下各自至少有一个关键点，求方案数。

$1 \le n \le 10^5$ 。

Solution

这篇Blog $O(n)$ 了，故提供一种更无脑一些的推柿子的方法。

一道奇怪的题，最终可以转化为无脑推柿子。

首先借一个题解区的图（图片来自这篇Blog）：

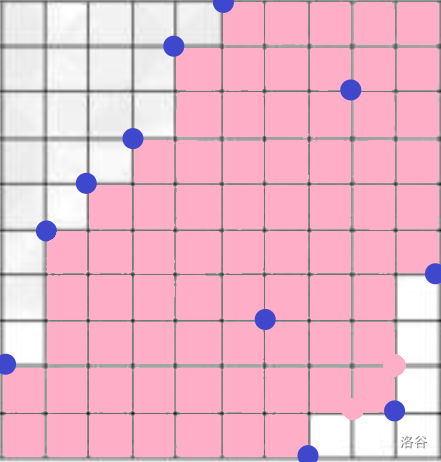
从Luogu搬的图，如果你看到这段文字那么说明Luogu的图挂了

$i$ $[l_i, r_i]$ $l_i$ 不在 $r_i$ 不在 $up_i$ $O(n^4)$ 点 $(i, j)$ $(x, y)$ 为左上端点，有答案为：

\begin{aligned} \sum_{i = 1}^{n} \sum_{j = l_{i}}^{r_{i}} \sum_{y = l_{i}}^{j - 1} \sum_{x = u p_{y}}^{i - 1} 1 & = \sum_{i = 1}^{n} \sum_{j = l_{i}}^{r_{i}} \sum_{y = l_{i}}^{j - 1} (i - u p_{y}) \\ = \sum_{i = 1}^{n} (\sum_{j = l_{i}}^{r_{i}} (j - l_{i}) i - \sum_{j = l_{i}}^{r_{i}} \sum_{y = l_{i}}^{j - 1} u p_{y}) \\ = \sum_{i = 1}^{n} (i (\frac{1}{2} (l_{i} + r_{i}) (r_{i} - l_{i} + 1) - (r_{i} - l_{i} + 1) l_{i}) - \sum_{j = l_{i}}^{r_{i}} \sum_{y = l_{i}}^{j - 1} u p_{y}) \\ = \sum_{i = 1}^{n} (i (\frac{1}{2} (r_{i} - l_{i}) (r_{i} - l_{i} + 1)) - \sum_{j = l_{i}}^{r_{i}} \sum_{y = l_{i}}^{j - 1} u p_{y}) \end{aligned}

$sum1_n = \sum_{i = 1}^{n}up_i$ $sum2_n = \sum_{i = 1}^{n}sum1_i$ ，有：

\begin{aligned} \sum_{i = 1}^{n} (i (\frac{1}{2} (r_{i} - l_{i}) (r_{i} - l_{i} + 1)) - \sum_{j = l_{i}}^{r_{i}} \sum_{y = l_{i}}^{j - 1} u p_{y}) \\ = & \sum_{i = 1}^{n} (i (\frac{1}{2} (r_{i} - l_{i}) (r_{i} - l_{i} + 1)) - \sum_{j = l_{i}}^{r_{i}} (s u m 1_{j - 1} - s u m 1_{l_{i} - 1})) \\ = & \sum_{i = 1}^{n} (i (\frac{1}{2} (r_{i} - l_{i}) (r_{i} - l_{i} + 1)) - \sum_{j = l_{i}}^{r_{i}} s u m 1_{j - 1} + (r_{i} - l_{i} + 1) s u m 1_{l_{i} - 1}) \\ = & \sum_{i = 1}^{n} (i (\frac{1}{2} (r_{i} - l_{i}) (r_{i} - l_{i} + 1)) - \sum_{j = l_{i} - 1}^{r_{i} - 1} s u m 1_{j} + (r_{i} - l_{i} + 1) s u m 1_{l_{i} - 1}) \\ = & \sum_{i = 1}^{n} (i (\frac{1}{2} (r_{i} - l_{i}) (r_{i} - l_{i} + 1)) - s u m 2_{r_{i} - 1} + s u m 2_{l_{i} - 2} + (r_{i} - l_{i} + 1) s u m 1_{l_{i} - 1}) \end{aligned}

$O(n^4)$ $O(n)$ 了。

Code


xxxxxxxxxx
72
1
#define _USE_MATH_DEFINES
2
#include <bits/extc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define SON i->to
8
#define OPNEW void* operator new(size_t)
9
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
10

11
using namespace std;
12
using namespace __gnu_pbds;
13

14
mt19937 rnd(random_device{}());
15
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
16
bool rnddd(int x){return rndd(1, 100) <= x;}
17

18
typedef unsigned int uint;
19
typedef unsigned long long unll;
20
typedef long long ll;
21
typedef long double ld;
22

23
#define MOD (ll)(1e9 + 7)
24
#define GetSum1(x) ((x) > 0 ? sum1[x] : 0)
25
#define GetSum2(x) ((x) > 0 ? sum2[x] : 0)
26

27
template< typename T = int >
28
inline T read(void);
29

30
int N;
31
int y[110000];
32
int l[110000], r[110000], up[110000];
33
ll sum1[110000];
34
ll sum2[110000];
35

36
int main(){
37
    N = read();
38
    for(int i = 1; i <= N; ++i){
39
        int rx = read() + 1, ry = read() + 1;
40
        y[rx] = ry;
41
    }l[0] = INT_MAX; r[N + 1] = -1;
42
    for(int i = 1; i <= N; ++i)l[i] = min(l[i - 1], y[i]);
43
    for(int i = N; i >= 1; --i)r[i] = max(r[i + 1], y[i]);
44
    int cur = r[1];
45
    for(int i = 1; i <= N; ++i)while(cur && cur >= l[i])up[cur] = i, --cur;
46
    for(int i = 1; i <= N; ++i)sum1[i] = (sum1[i - 1] + up[i]) % MOD;
47
    for(int i = 1; i <= N; ++i)sum2[i] = (sum2[i - 1] + sum1[i]) % MOD;
48
    ll ans(0);
49
    for(int i = 1; i <= N; ++i){
50
        ans = (ans + ((ll)r[i] - l[i]) * (r[i] - l[i] + 1) / 2ll % MOD * i % MOD) % MOD;
51
        ans = (ans - GetSum2(r[i] - 1) + GetSum2(l[i] - 2) + MOD) % MOD;
52
        ans = (ans + ((ll)r[i] - l[i] + 1) * GetSum1(l[i] - 1) % MOD) % MOD;
53
    }printf("%lld\n", ans);
54
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
55
    return 0;
56
}
57

58
template < typename T >
59
inline T read(void){
60
    T ret(0);
61
    short flag(1);
62
    char c = getchar();
63
    while(c != '-' && !isdigit(c))c = getchar();
64
    if(c == '-')flag = -1, c = getchar();
65
    while(isdigit(c)){
66
        ret *= 10;
67
        ret += int(c - '0');
68
        c = getchar();
69
    }
70
    ret *= flag;
71
    return ret;
72
}

UPD

update-2022_11_03 初稿

LG-P4184 [USACO18JAN]Sprinklers P Solution

更好的阅读体验戳此进入

题面

Solution

Code

UPD