LG-P3549 [POI2013]MUL-Multidrink Solution

更好的阅读体验戳此进入

（建议您从上方链接进入我的个人网站查看此 Blog，在 Luogu 中图片会被墙掉，部分 Markdown 也会失效）

题面

一道论文题。

给定一棵有 $n$$n$ 个节点的树，令起点为 $1$$1$，终点为 $n$$n$，每步可以走的距离为 $1$$1$ 或 $2$$2$，要求不重复地遍历 $n$$n$ 个节点。

如果无解输出 BARK，否则输出 $n$$n$ 行，表示遍历的路径，存在 SPJ。

$1\le n\le 5\times {10}^5$$1 \le n \le 5 \times 10^5$。

输入格式

$n$$n$

Describe the tree($n-1$$n - 1$ lines in total).

图例

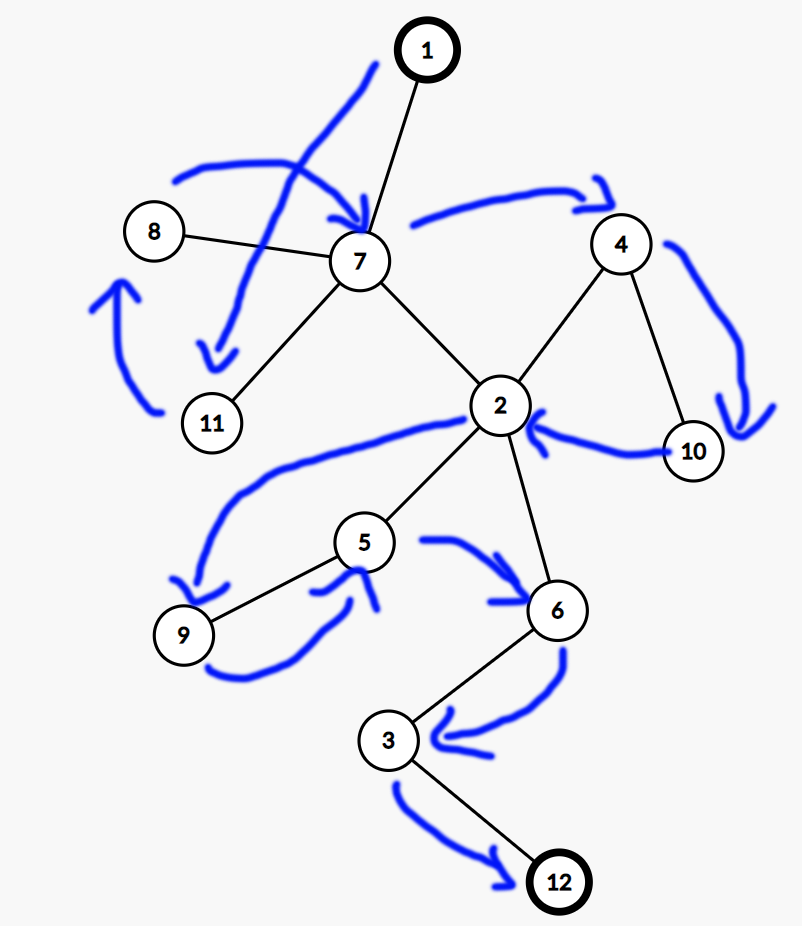
Solution

本题大多数内容均参考自论文《Hamiltonian paths in the square of a tree》。

作者：Jakub Radoszewski and Wojciech Rytter。

原文链接：Hamiltonian paths in the square of a tree

首先我们引入一个定义：caterpillar（毛毛虫），原文定义为 a single path with several leafs connected to it. 简而言之就是其为一棵树，一棵树为 caterpillar 当且仅当去掉其所有叶子节点后剩下的仅为一条单链，如图即为一个 caterpillar。

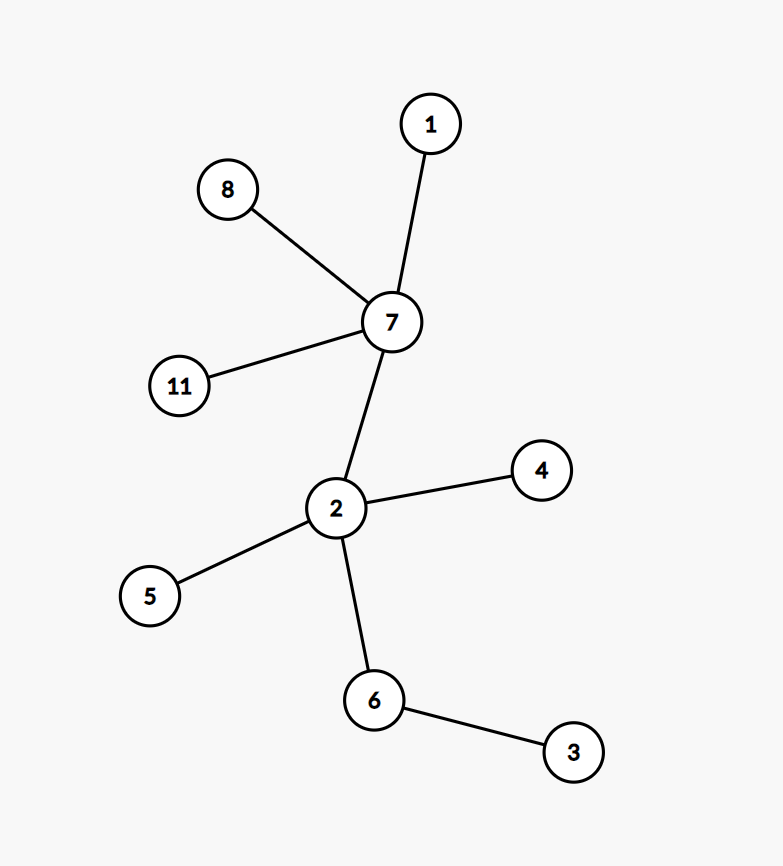
对于其更多的性质及求法，可以去做一下 LG-P3174 [HAOI2009] 毛毛虫，但与本题关联不大，就不再赘述。

现在我们引入下一个定义，对于图 $G=(V,E)$$G = (V, E)$，我们定义 $G$$G$ 的 $k$$k$ 次幂，记作 $G^k$$G^k$，为一个基于（或者说完全覆盖，原文为 cover）点集 $V$$V$ 的图，对于 $\mathrm{\forall }u,v\in V$$\forall u, v \in V$，$u,v$$u, v$ 之间有边相连当且仅当在 $G$$G$ 中 $u,v$$u, v$ 之间的路径长度不大于 $k$$k$。我们称 $G^2$$G^2$ 为 the square of $G$$G$，称 $G^3$$G^3$ 为 the cube of $G$$G$。

然后我们再引入一个定义：2-connected graph（2-连通图），这个定义类似点双，对于具有割点的图我们定义其为 1-connected graph，则同理 2-connected graph 只得就是至少需要去掉两个顶点才能使图的连通分支增加。

现在我们再引入几个定理：

Lemma 1：对于树 $T$$T$，图 $T^2$$T^2$ 包含哈密尔顿回路当且仅当 $T$$T$ 为一个 caterpillar。

Lemma 2：对于树 $T$$T$，图 $T^2$$T^2$ 包含哈密尔顿路径当且仅当 $T$$T$ 为一个 horsetail。

证明：咕咕咕。

然后我们继续进行定义。

定义 $P$$P$ 为 $G$$G$ 的 k-path 当且仅当 $P$$P$ 为 $G^k$$G^k$ 中的一条路径，同理我们定义 k-cycle。

额外地，我们分别定义 $G$$G$ 的 kH-path 和 kH-cycle 为 $G^k$$G^k$ 中的哈密尔顿路径和哈密尔顿回路。

若 $G^k$$G^k$ 包含一个 kH-cycle，我们称 $G$$G$ 为 k-Hamiltonian（这玩意我也不知道怎么译），同理包含 kH-path 称为 k-traceable。

然后对于 caterpillar，我们额外定义其为 non-trivial 当且仅当其至少含有 $1$$1$ 条边。

我们称 caterpillar 的主链，也就是去掉叶子结点剩下的链，为 spine。

下面开始正文：

我们考虑将原图中 $1$$1$ 到 $n$$n$ 的路径抽离出来，作为其主干，然后将主干上每个点及其每个子树作为一个新的部分，这里有一个性质，对于这些非主干的部分，有一个性质：若其非 caterpillar，则一定无解，这个东西自己画一下找找性质就会发现很显然，当然严谨的证明我不会。

然后这里我们对于每个主干上的点划分为两类：

1. Type A：有不超过 $1$$1$ 个 non-trivial caterpillar。
2. Type B：有且仅有 $2$$2$ 个 non-trivial caterpillar。

不难发现，对于 Type A 的节点，若从主干上的节点进入，最后一步一定刚好走到下一个主干节点上，对于 Type B 的节点，在进入时必须直接进入到其任意子树中，否则无解，对于后面的无解判断我们主要也就靠这个性质。

这里有一个性质：若一个点有超过两个的 non-trivial caterpillar 则一定无解，这个依然，自己画一下会发现无论上一步刚好走到这个点还是直接走到某一个子树上，最终都是无解的，路径一定会断在某个子树中，同样严谨的证明我不会。

然后我们额外地定义一个点为 free 当且仅当其为单点，即没有任何子树的主干节点。

如下图例：

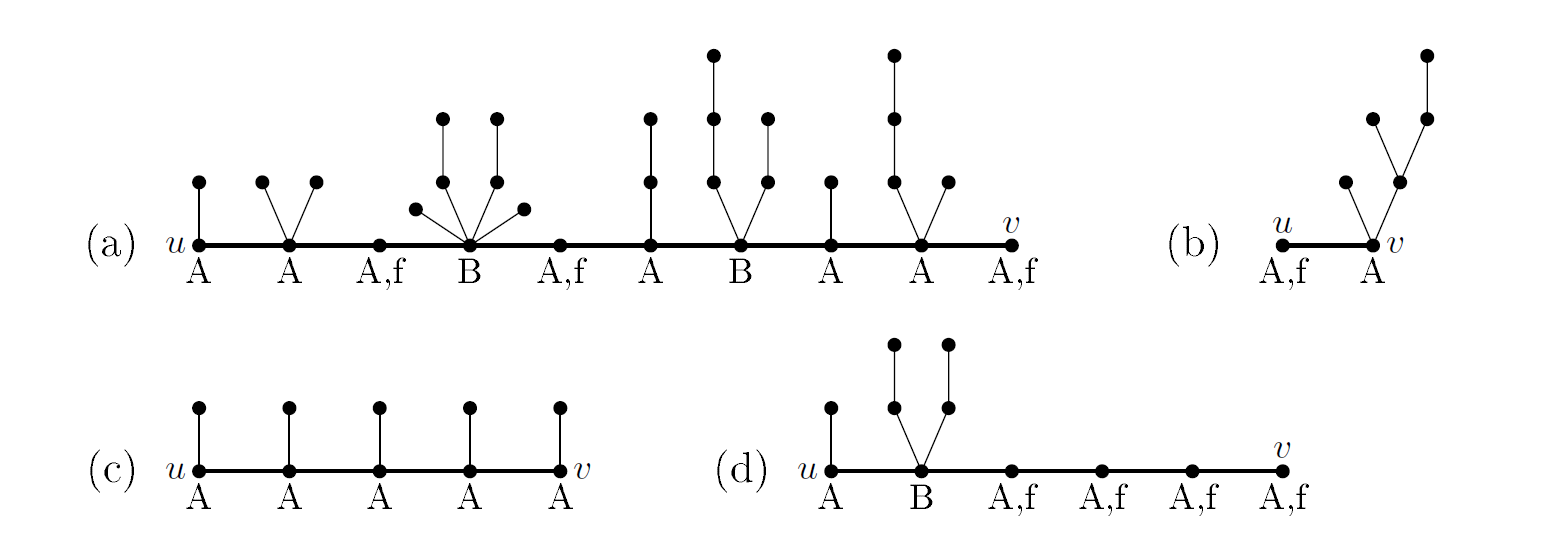
下一个性质：每个 Type B 的节点前后都必须有至少一个 free 节点，否则无解。显然 free 点是可以将进入下一个主干节点和进入下一个主干节点的某一个子节点相互转换的，而 Type A 不能进行这样的转换，两棵 Type B 之间又需要有这样的转换。

对于满足以上所有性质的主干，我们称其为 $(u,v)$$(u, v)$ -horsetail，同时称这整棵树为 horsetail。

现在我们对上面的性质做一个总结：

1. 每一个主干节点都为 Type A 或 Type B。
2. 在任意两个 Type B 之间都至少有一个 free。
3. 在 Type B 之前至少有一个 free。
4. 在 Type B 之后至少有一个 free。
5. 至少有一个 free。

显然对于上面的四个图例中，(a)(b) 为 horsetail，有解，(c)(d) 非 horsetail，无解。

而对于我们本题的图 $G$$G$，我们也就需要先判断其是否为 horsetail，如果不是则无解，如果是那么说明 $G^2$$G^2$，也就是按照本题要求构成的图，一定存在一条哈密顿路径，即 Lemma 2。

现在我们对 Lemma 1 进行进一步的阐释：

Lemma 1：任意一个在 caterpillar 上的 2H-cycle 都一定有以下的顺序：我们定义 caterpillar 的 spine 长度为 $l$$l$，令 spine 为 $v_1,v_2,\cdots ,v_l$$v_1, v_2, \cdots, v_l$，spine 上的叶子为 $P_1,P_2,\cdots ,P_l$$P_1, P_2, \cdots, P_l$，这里我们定义 $P_i$$P_i$ 表示一个任意的 $v_i$$v_i$ 的叶子的排列。

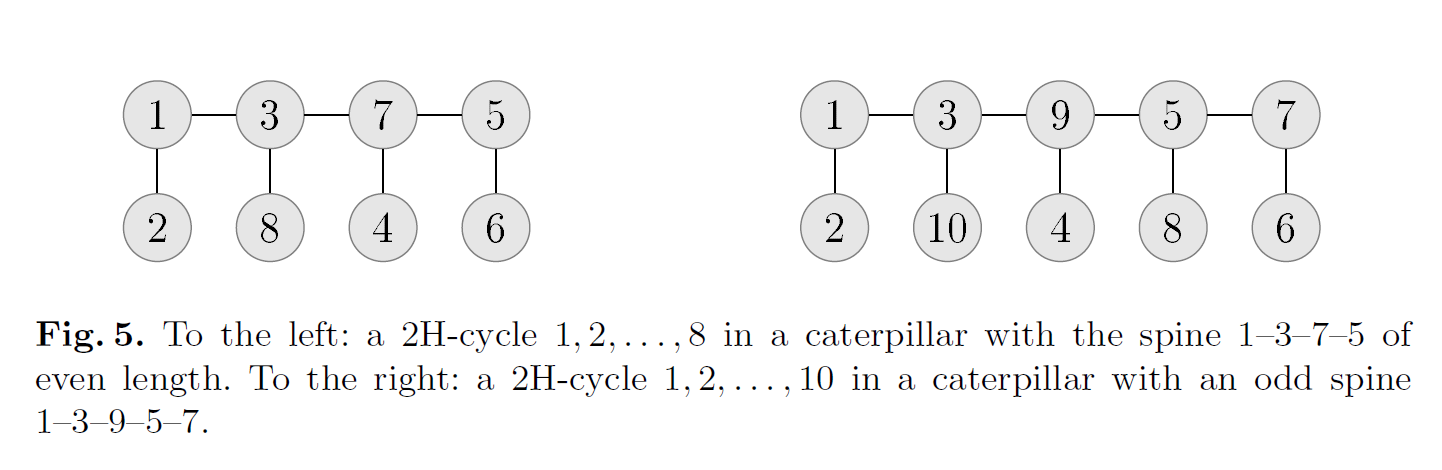
如此图中，显然 $1,2,3,\cdots ,8,1$$1, 2, 3, \cdots, 8, 1$ 和 $1,2,3,\cdots ,10,1$$1, 2, 3, \cdots, 10, 1$ 分别为两图的一种 2H-cycle。

所以当我们想要对 horsetail 上的 caterpillar 找到 2H-path 的时候，只需要取 2H-cycle 中的一部分，或者说断开 2H-cycle 中的一条边，如 $2,3,4,\cdots ,8,1$$2, 3, 4, \cdots, 8, 1$ 这种顺序。

然后再次回到本题，或者说回到 Lemma 2：

对于一个 2H-path $S$$S$，当树 $T$$T$ 上的节点被按照分别遍历每个主干节点的每个子树的顺序遍历时，同时我们定义每个主干节点 $u_i$$u_i$ 所在子树节点集合为 $layer(u_i)$$layer(u_i)$，满足每个 $layer(u_i)$$layer(u_i)$ 都按照特定顺序遍历，我们称树 $T$$T$ 为 layered，此时我们便可以根据每个主干节点的路径将 $S$$S$ 分成 $S_1,S_2,S_3,\cdots$$S_1, S_2, S_3, \cdots$。我们定义一个路径 $S$$S$ 的起点和终点分别为 $first(S)$$first(S)$ 和 $last(S)$$last(S)$，定义主干节点为 main，主干节点直接连接的非主干节点为 secondary，则显然对于每个 $i$$i$，$first(S_i)$$first(S_i)$ 和 $last(S_i)$$last(S_i)$ 均为 main 或 secondary。

对于我们的算法我们首先需要实现一些辅助函数：（为了便于理解，部分函数名与原论文中有微调）

vector < int > BuildCaterpillar(int mp, int S, int T)：

对于从 $S$$S$ 开始 $T$$T$ 结束的，挂在 horsetail 的主干上的 $1$$1$ 或 $2$$2$ 条 caterpillar 生成 2H-path，这里我们首先需要对这一部分构建一个新的图，将 caterpillar 上所有叶子指向 spine，同时我们需要维护每条 caterpillar 的主干，具体通过代码中的 void BuildSpine(int fa, int p) 实现，我们称 caterpillar 所在的 horsetail 上的主干节点为 $mp$$mp$，那么当 $mp$$mp$ 为 type B 的时候，也就是 non-trivial 的 caterpillar 有两条的时候，我们便可以将前面一条 caterpillar 反过来与其首尾相接，当成同一条 caterpillar，这样最终我们对于形成的 caterpillar 进行如 Lemma 1 地生成 2H-cycle，然后断开其中 $S\to T$$S \rightarrow T$ 的边（或 $T\to S$$T \rightarrow S$）即可，同时需要注意如果起始点是在非 non-trivial 的 secondary 节点上，那么我们就需要先遍历其叶子节点，然后最后再遍历其 spine，对于遍历 $mp$$mp$ 的叶子节点，我们通过 void extend(int mp, int unreach1 = -1, int unreach2 = -1) 实现，具体可以看一下代码。

int FindAnySecondaryNode(int p)：找到 horsetail 中主干为 $p$$p$ 的任意一个 secondary 节点。

int FindAnySecondaryNode_PreferablyLeaf(int p)：找到 horsetail 中主干为 $p$$p$ 的任意一个 secondary 节点，且优先找非 non-trivial 的叶子节点。

int FindAnotherSecondaryNode(int p, int lst)：找到 horsetail 中主干为 $p$$p$ 的非 $lst$$lst$ 的另一个 secondary 节点。

然后对于具体的实现，首先我们需要检查一下其是否为无解，也就是前面的检查是否为 horsetail，具体由 void Check(void) 实现。

然后我们算法的核心就是找到 horsetail 的那一条 2H-path，通过 vector < int > Get2HPathHorsetail(void) 实现，大概的思路就是先对第一个节点进行讨论，显然起点一定为 $1$$1$，如果其为 free 节点那么终点也为 $1$$1$，否则一定为其的某一个 secondary 节点，然后构造此 2H-path，对于后面的每个点，如果是 free 节点那么起点终点均为主干点 $mp$$mp$，否则如果上次的终点不是主干节点，这次的起点一定为 $mp$$mp$，终点为优先找非 non-trivial 节点的任意一个 secondary 节点，如果上次的终点是主干节点，那么这次的起点一定为优先找非 non-trivial 节点的 secondary 节点，对于终点，如果该节点是 type B，那么终点也需要为 secondary 节点，找到另外的一个 secondary 节点即可，否则终点为 $mp$$mp$ 即可。

大致的思路就是这样，码量大概 7.5KiB，随后的复杂度是 linear 的，也就是 $O(n)$$O(n)$ 的。

同时这里提供一个原论文中的对于最后的 Get2HPathHorsetail(void) 的实现，可以选择性地看一下。

Code

x
1
#define _USE_MATH_DEFINES
2
#include <bits/extc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define SON i->to
8
#define OPNEW void* operator new(size_t)
9
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
10

11
/******************************
12
abbr
13
mp => mainp
14
subt => subtree
15
fa => father
16
fst => first
17
lst => last
18
******************************/
19

20
using namespace std;
21
using namespace __gnu_pbds;
22

23
mt19937 rnd(random_device{}());
24
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
25
bool rnddd(int x){return rndd(1, 100) <= x;}
26

27
typedef unsigned int uint;
28
typedef unsigned long long unll;
29
typedef long long ll;
30
typedef long double ld;
31

32
#define EXIT puts("BRAK"), exit(0)
33
#define MAXN 510000
34

35
template<typename T = int>
36
inline T read(void);
37

38
struct Edge{
39
    Edge* nxt;
40
    int to;
41
    OPNEW;
42
}ed[(MAXN << 1) + MAXN];
43
ROPNEW(ed);
44
Edge* head[MAXN];
45

46
int N;
47
int mainLen(0);
48
int fa[MAXN], deg[MAXN];
49
int mainp[MAXN];
50
int non_trivial[MAXN];
51
bool isMainp[MAXN], isFree[MAXN];
52

53
void dfs(int p = 1){
54
    for(auto i = head[p]; i; i = i->nxt)
55
        if(SON != fa[p])
56
            fa[SON] = p,
57
            dfs(SON);
58
}
59
void InitMainp(void){
60
    int cur = N;
61
    do{
62
        mainp[++mainLen] = cur;
63
        isMainp[cur] = true;
64
        cur = fa[cur];
65
    }while(cur != 1);
66
    mainp[++mainLen] = 1;
67
    isMainp[1] = true;
68
    reverse(mainp + 1, mainp + mainLen + 1);
69
}
70
bool isCaterpillar(int fa, int p){
71
    int cnt(0);
72
    for(auto i = head[p]; i; i = i->nxt){
73
        if(SON == fa || deg[SON] == 1)continue;
74
        if(!isCaterpillar(p, SON))return false;
75
        if(cnt++)return false;
76
    }return true;
77
}
78
void Check(void){
79
    for(int p = 1; p <= mainLen; ++p){
80
        int mp = mainp[p];
81
        isFree[mp] = true;
82
        for(auto i = head[mp]; i; i = i->nxt){
83
            if(isMainp[SON])continue;
84
            isFree[mp] = false;
85
            if(deg[SON] == 1)continue;
86
            ++non_trivial[mp];
87
            if(non_trivial[mp] > 2)EXIT;
88
            if(!isCaterpillar(mp, SON))EXIT;
89
        }
90
    }
91
    int curFree(0);
92
    bool end_with_B(true);
93
    bool exist_free(false);
94
    for(int p = 1; p <= mainLen; ++p){
95
        int mp = mainp[p];
96
        if(isFree[mp]){++curFree; exist_free = true; end_with_B = false; continue;}
97
        if(non_trivial[mp] == 2){
98
            if(!curFree)EXIT;
99
            curFree = 0;
100
            end_with_B = true;
101
        }
102
    }
103
    if(end_with_B || !exist_free)EXIT;
104
}
105
int FindAnySecondaryNode(int p){
106
    for(auto i = head[p]; i; i = i->nxt)
107
        if(!isMainp[SON])return SON;
108
    return -1;
109
}
110
int FindAnySecondaryNode_PreferablyLeaf(int p){
111
    for(auto i = head[p]; i; i = i->nxt)
112
        if(!isMainp[SON] && deg[SON] == 1)return SON;
113
    return FindAnySecondaryNode(p);
114
}
115
int FindAnotherSecondaryNode(int p, int lst){
116
    for(auto i = head[p]; i; i = i->nxt)
117
        if(!isMainp[SON] && SON != lst)return SON;
118
    return -1;
119
}
120
namespace Caterpillar{
121
    vector < int > route;
122
    Edge* head[MAXN];
123
    vector < int > spine;
124
    enum type{spineNode = 1, leafNode};
125
    int ffa[MAXN];
126
    void add(int s, int t){
127
        head[s] = new Edge{head[s], t};
128
        ffa[t] = s;
129
    }
130
    void BuildSpine(int fa, int p){
131
        spine.push_back(p);
132
        for(auto i = ::head[p]; i; i = i->nxt){
133
            if(SON == fa)continue;
134
            if(::deg[SON] == 1)add(p, SON);
135
            else BuildSpine(p, SON);
136
        }
137
    }
138
    void extend(int mp, int unreach1 = -1, int unreach2 = -1){
139
        for(auto i = head[mp]; i; i = i->nxt){
140
            if(SON == unreach1 || SON == unreach2)continue;
141
            route.push_back(SON);
142
        }
143
    }
144
    vector < int > BuildCaterpillar(int mp, int S, int T){
145
        route.clear();
146
        spine.clear();
147
        route.push_back(S);
148
        if(S == T)return route;
149
        spine.push_back(mp);
150
        bool exist_caterpillar(false);
151
        for(auto i = ::head[mp]; i; i = i->nxt){
152
            if(isMainp[SON])continue;
153
            if(deg[SON] == 1)add(mp, SON);
154
            else{
155
                if(!exist_caterpillar)exist_caterpillar = true;
156
                else reverse(spine.begin(), spine.end());
157
                BuildSpine(mp, SON);
158
            }
159
        }
160
        vector < pair < int, type >/*spine_node_pos, spine or leaf*/ > temp;
161
        vector < pair < int, type >/*spine_node_pos, spine or leaf*/ > unextended;
162
        for(int i = 0; i < (int)spine.size(); ++i)
163
            temp.push_back({spine.at(i), !(i & 1) ? spineNode : leafNode});
164
        for(int i = (int)spine.size() - 1; i >= 0; --i)
165
            temp.push_back({spine.at(i), (i & 1) ? spineNode : leafNode});
166
        for(auto it = temp.begin(); it < temp.end(); ++it)
167
            if(it->second == spineNode || head[it->first])unextended.push_back(*it);
168
        #define LEFT(x) (x == 0 ? (int)unextended.size() - 1 : x - 1)
169
        #define RIGHT(x) (x == (int)unextended.size() - 1 ? 0 : x + 1)
170
        auto Beg = deg[S] == 1 ? make_pair(ffa[S], leafNode) : make_pair(S, spineNode);
171
        auto End = deg[T] == 1 ? make_pair(ffa[T], leafNode) : make_pair(T, spineNode);
172
        int begPos = -1; while(unextended.at(++begPos) != Beg);
173
        if(Beg.second == leafNode)extend(Beg.first, S, T);
174
        if(unextended.at(LEFT(begPos)) == End)
175
            for(int j = RIGHT(begPos); unextended.at(j) != End; j = RIGHT(j))
176
                unextended.at(j).second == spineNode
177
                    ? route.push_back(unextended.at(j).first)
178
                    : extend(unextended.at(j).first);
179
        else
180
            for(int j = LEFT(begPos); unextended.at(j) != End; j = LEFT(j))
181
                unextended.at(j).second == spineNode
182
                    ? route.push_back(unextended.at(j).first)
183
                    : extend(unextended.at(j).first);
184
        if(End.second == leafNode && Beg != End)extend(End.first, S, T);
185
        route.push_back(T);
186
        return route;
187
    }
188
}
189
vector < int > Get2HPathHorsetail(void){
190
    vector < int > ret;
191
    int fst = mainp[1];
192
    int lst = isFree[mainp[1]]
193
        ? mainp[1]
194
        : FindAnySecondaryNode(mainp[1]);
195
    auto tmp = Caterpillar::BuildCaterpillar(mainp[1], fst, lst);
196
    ret.insert(ret.end(), tmp.begin(), tmp.end());
197
    for(int i = 2; i <= mainLen; ++i){
198
        int w = mainp[i];
199
        if(isFree[w])fst = lst = w;
200
        else if(!isMainp[lst])
201
            fst = w,
202
            lst = FindAnySecondaryNode_PreferablyLeaf(w);
203
        else
204
            fst = FindAnySecondaryNode_PreferablyLeaf(w),
205
            lst = non_trivial[w] == 2
206
                ? FindAnotherSecondaryNode(w, fst)
207
                : w;
208
        auto cp = Caterpillar::BuildCaterpillar(w, fst, lst);
209
        ret.insert(ret.end(), cp.begin(), cp.end());
210
    }
211
    return ret;
212
}
213
int main(){
214
    N = read();
215
    for(int i = 1; i <= N - 1; ++i){
216
        int s = read(), t = read();
217
        head[s] = new Edge{head[s], t};
218
        head[t] = new Edge{head[t], s};
219
        ++deg[s], ++deg[t];
220
    }
221
    dfs();
222
    InitMainp();
223
    Check();
224
    auto ans = Get2HPathHorsetail();
225
    for(auto i : ans)printf("%d\n", i);
226
    return 0;
227
}
228
template<typename T>
229
inline T read(void){
230
    T ret(0);
231
    short flag(1);
232
    char c = getchar();
233
    while(c != '-' && !isdigit(c))c = getchar();
234
    if(c == '-')flag = -1, c = getchar();
235
    while(isdigit(c)){
236
        ret *= 10;
237
        ret += int(c - '0');
238
        c = getchar();
239
    }
240
    ret *= flag;
241
    return ret;
242
}

写在后面

就是这道不怎么友好的题，我做的时候网上几乎没有题解，只能找到几篇说的很简略的题解，然后没办法只能去自己翻英文论文，然后一个一个查词，在我快要写完这道题的时候，才突然发现 Luogu 上多出来了两篇题解。。

然后就是调这道题，一共交了 $70+$$70+$ 次才过了这道题，自己写完之后怎么改都是 $70$$70$ pts，Luogu 上下不了数据，hydro 等没有 SPJ，没办法只能开始把每一部分的代码对着大佬的代码改，最后几乎把整篇代码都重构了一遍才找到错误，只是调代码就调了一天半，不过至少最后还是过了。

UPD

update-2022_10_09 初稿

update-2022_10_10 修复一些错误