FFT & NTT - 快速傅里叶变换 & 快速数论变换
FFT & NTT - 快速傅里叶变换 & 快速数论变换更好的阅读体验戳此进入写在前面目的前置知识原根单位根模意义下的(原根)复数意义下的单位根性质单位根求法复数意义下模意义下的(原根)等比数列求和公式正文单位根反演推式子继续推式子Code优化NTT合并DFT优化写在后面UPD
更好的阅读体验戳此进入
(建议您从上方链接进入我的个人网站查看此 Blog,在 Luogu 中图片会被墙掉,部分 Markdown 也会失效)
写在前面
该博客仅为记录学习中的笔记及个人理解,不保证正确性,同时欢迎各位纠正。
图片没有放在图床上,全都是丢在自己的网站上,带宽较低可能加载较慢。
目的
FFT (Fast Fourier Transform) 是为了为快速求出两个多项式的卷积,也就是
(
前置知识
原根
详细定义可参考 知乎 或 OI-WIKI,简而言之就是,对于模
单位根
对于
模意义下的(原根)
对于模
更通俗一点的描述,也就是对于所有
证明:
由 费马小定理 可知显然成立
复数意义下的
对于复数意义下的,则可将一单位圆 n 等分,并取该 n 个点表示的复数,从 x 轴,也就是从
很多地方可能用
单位根性质
对于复数意义下的
证明
单位根求法
复数意义下
由单位根的定义显然可知对于 n 次单位根的 k 次方,即
模意义下的(原根)
因为 NTT 模数的原根一般都很小,只有极少数的质数的原根能达到 20,所以可以直接按照定义,考虑遍历所有
同时还存在一种效率更高的方式,考虑将
等比数列求和公式
正文
单位根反演
对于
又有
且又有如下式子
综上则有如下式子
此即为单位根反演
推式子
将单位根反演代入原式,令
且令
显然有如下式子
观察最后两个式子,可以发现如下两个式子
考虑令该多项式上一点为
证明
则可知求
由定义显然有
(
又有
证明
则此时多项式 C 可求,但时间复杂度仍然是
继续推式子
对于
可以考虑
且令
由单位根的性质可以得到以下式子
其中u为一个二次单位根,因为显然当且仅当
此时显然有
且我们已知
所以
此时可以考虑令
所以将幂次除以二后,显然有(此时
再将式子转化为
此时式子形式便可按相同方法继续递归,直到
Code
xxxxxxxxxx981
4
10
12/******************************13abbr14pat -> pattern15pol/poly -> polynomial16omg -> omega17******************************/18
19using namespace std;20
21mt19937 rnd(random_device{}());22int rndd(int l, int r){return rnd() % (r - l + 1) + l;}23
24typedef unsigned int uint;25typedef unsigned long long unll;26typedef long long ll;27
28class Polynomial{29 private:30 int lena, lenb;31 int len;32 comp A[1100000], B[1100000];33 public:34 comp Omega(int, int, bool);35 void Init(void);36 void FFT(comp*, int, bool);37 void MakeFFT(void);38}poly;39
40template<typename T = int>41inline T read(void);42
43int main(){44 poly.Init();45 poly.MakeFFT();46
47 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);48 return 0;49}50void Polynomial::MakeFFT(void){51 FFT(A, len, DFT), FFT(B, len, DFT);52 for(int i = 0; i <= len; ++i)A[i] *= B[i];53 FFT(A, len, IDFT);54 for(int i = 0; i <= lena + lenb - 2; ++i)55 printf("%d%c", int(A[i].real() / len + eps + 0.5), i == lena + lenb - 1 ? '\n' : ' ');56}57void Polynomial::FFT(comp* pol, int len, bool pat){58 if(len == 1)return;59 comp sA[len / 2 + 10], sB[len / 2 + 10];60 for(int i = 0; i <= len / 2 - 1; ++i){61 sA[i] = pol[i * 2];62 sB[i] = pol[i * 2 + 1];63 }64 FFT(sA, len / 2, pat), FFT(sB, len / 2, pat);65 for(int i = 0; i <= len / 2 - 1; ++i){66 comp omg = Omega(len, i, pat);67 pol[i] = sA[i] + omg * sB[i];68 pol[i + len / 2] = sA[i] - omg * sB[i];69 }70}71void Polynomial::Init(void){72 lena = read(), lenb = read();73 for(int i = 0; i <= lena; ++i)A[i].real((double)read());74 for(int i = 0; i <= lenb; ++i)B[i].real((double)read());75 len = 1;76 lena++, lenb++;77 while(len <= lena + lenb)len <<= 1;78}79comp Polynomial::Omega(int n, int k, bool pat){80 if(pat == DFT)return comp(cos(2 * PI * k / n), sin(2 * PI * k / n));81 return conj(comp(cos(2 * PI * k / n), sin(2 * PI * k / n)));82}83
84template<typename T>85inline T read(void){86 T ret(0);87 short flag(1);88 char c = getchar();89 while(c != '-' && !isdigit(c))c = getchar();90 if(c == '-')flag = -1, c = getchar();91 while(isdigit(c)){92 ret *= 10;93 ret += int(c - '0');94 c = getchar();95 }96 ret *= flag;97 return ret;98}优化
显然递归版本的写法虽然更容易理解,但每层都需要开额外的数组,消耗空间很大,时间也较大,虽然可以通过 洛谷模板,但是在后面的题里可能会被卡常,于是便有了如下的优化,即
首先观察如下递归过程( 图片来源 )
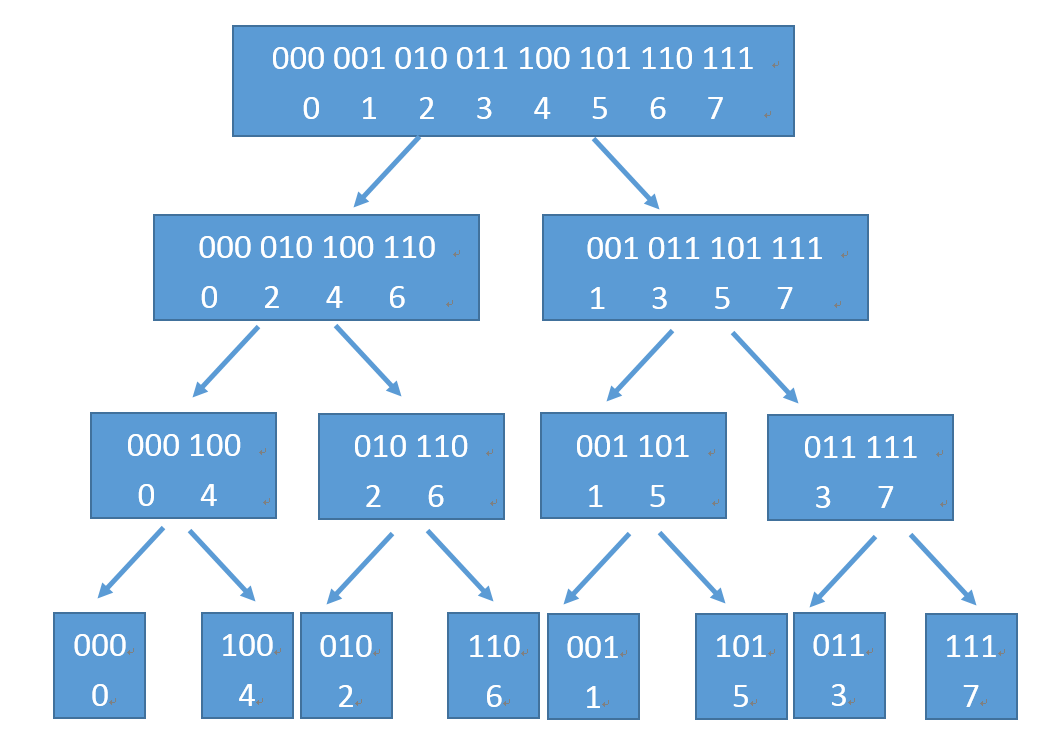
通过观察我们即可发现(这真是人类能想出来的吗)对于每一个数的位置,显然是进行了一次二进制的反转,如 1 的位置从 001 变成了 100,那么我们便可以利用这个性质对位置进行反转。
这里提供两种写法
xxxxxxxxxx91int size(0);2while((1 << size) < len - 1)++size;3for(int i = 0; i <= len - 1; ++i){4 int tmp(0);5 for(int j = 0; j <= size; ++j){6 if((1 << j) & i) tmp |= (1 << (size - j - 1));7 }8 if(i < tmp)swap(pol[i], pol[tmp]);9}类似于模拟的写法,首先判断二进制数的位数,即 size,然后对于每个数按位判断,并将其转移到 tmp 的对应位置,最后通过swap交换位置,
xxxxxxxxxx71int pos[len + 10];2memset(pos, 0, sizeof(pos));3for(int i = 0; i < len; ++i){4 pos[i] = pos[i >> 1] >> 1;5 if(i & 1)pos[i] |= len >> 1;6}7for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);这种方法我就不严格地证明了(主要我也不会),就从找规律的角度来研究一下这个线性递推的式子。
举个例子,假设我们有一个二进制数
对于 Reverse 后合并的过程显然我们可以通过从倒数第二层开始,模拟递归形式的操作,这部分较为显然便不再赘述。
值得注意的一个点是当我们更新数组时,由于非递归写法,可能会对需要用到的变量进行覆盖,所以这时我们显然可以将原数组复制一份,这样的空间时可以接受的,当然更好的做法就是将会被覆盖的那个变量存起来再进行操作,如下。
xxxxxxxxxx111Reverse(pol, len);2for(int size = 2; size <= len; size <<= 1){3 for(comp* p = pol; p != pol + len; p += size){4 int mid(size >> 1);5 for(int i = 0; i < mid; ++i){6 auto tmp = Omega(size, i, pat) * p[i + mid];7 p[i + mid] = p[i] - tmp;8 p[i] = p[i] + tmp;9 }10 }11}最后贴上优化后的完整代码
xxxxxxxxxx1081
5
11
13/******************************14abbr15pat -> pattern16pol/poly -> polynomial17omg -> omega18******************************/19
20using namespace std;21
22mt19937 rnd(random_device{}());23int rndd(int l, int r){return rnd() % (r - l + 1) + l;}24
25typedef unsigned int uint;26typedef unsigned long long unll;27typedef long long ll;28
29class Polynomial{30 private:31 int lena, lenb;32 int len;33 comp A[2100000], B[2100000];34 public:35 comp Omega(int, int, bool);36 void Init(void);37 void FFT(comp*, int, bool);38 void Reverse(comp*);39 void MakeFFT(void);40}poly;41
42template<typename T = int>43inline T read(void);44
45int main(){46 poly.Init();47 poly.MakeFFT();48
49 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);50 return 0;51}52void Polynomial::MakeFFT(void){53 FFT(A, len, DFT), FFT(B, len, DFT);54 for(int i = 0; i <= len; ++i)A[i] *= B[i];55 FFT(A, len, IDFT);56 for(int i = 0; i <= lena + lenb - 2; ++i)57 printf("%d%c", int(A[i].real() / len + eps + 0.5), i == lena + lenb - 2 ? '\n' : ' ');58}59void Polynomial::Reverse(comp* pol){60 int pos[len + 10];61 memset(pos, 0, sizeof(pos));62 for(int i = 0; i < len; ++i){63 pos[i] = pos[i >> 1] >> 1;64 if(i & 1)pos[i] |= len >> 1;65 }66 for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);67}68void Polynomial::FFT(comp* pol, int len, bool pat){69 Reverse(pol);70 for(int size = 2; size <= len; size <<= 1){71 for(comp* p = pol; p != pol + len; p += size){72 int mid(size >> 1);73 for(int i = 0; i < mid; ++i){74 auto tmp = Omega(size, i, pat) * p[i + mid];75 p[i + mid] = p[i] - tmp;76 p[i] = p[i] + tmp;77 }78 }79 }80}81void Polynomial::Init(void){82 lena = read(), lenb = read();83 for(int i = 0; i <= lena; ++i)A[i].real((double)read());84 for(int i = 0; i <= lenb; ++i)B[i].real((double)read());85 len = 1;86 lena++, lenb++;87 while(len <= lena + lenb)len <<= 1;88}89comp Polynomial::Omega(int n, int k, bool pat){90 if(pat == DFT)return comp(cos(2 * PI * k / n), sin(2 * PI * k / n));91 return conj(comp(cos(2 * PI * k / n), sin(2 * PI * k / n)));92}93
94template<typename T>95inline T read(void){96 T ret(0);97 short flag(1);98 char c = getchar();99 while(c != '-' && !isdigit(c))c = getchar();100 if(c == '-')flag = -1, c = getchar();101 while(isdigit(c)){102 ret *= 10;103 ret += int(c - '0');104 c = getchar();105 }106 ret *= flag;107 return ret;108}NTT
前面我们已知 FFT 是在复数意义下利用单位复根的性质进行优化,而 NTT 则是在模意义下的,对于模意义下的单位根替代品则为原根,至于证明这里不再赘述,可以在 此处 查看。
而对于如洛谷模板题的这种答案系数较小的,我们可以考虑用 NTT 代替 FFT 以大量减少时间空间消耗,我们只需要找到一个比最大的答案(
实现过程中只需要根据结论,用原根代替单位根,如将
Code:
xxxxxxxxxx1161
5
12/******************************13abbr14pat -> pattern15pol/poly -> polynomial16******************************/17
18using namespace std;19
20mt19937 rnd(random_device{}());21int rndd(int l, int r){return rnd() % (r - l + 1) + l;}22
23typedef unsigned int uint;24typedef unsigned long long unll;25typedef long long ll;26
27ll kpow(int a, int b){28 ll ret(1ll), mul((ll)a);29 while(b){30 if(b & 1)ret = (ret * mul) % MOD;31 b >>= 1;32 mul = (mul * mul) % MOD;33 }34 return ret;35}36class Polynomial{37 private:38 int lena, lenb;39 int len;40 int g, inv_g;41 int A[2100000], B[2100000];42 public:43 int Omega(int, int, bool);44 void Init(void);45 void NTT(int*, int, bool);46 void Reverse(int*);47 void MakeNTT(void);48}poly;49
50template<typename T = int>51inline T read(void);52
53int main(){54 poly.Init();55 poly.MakeNTT();56 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);57 return 0;58}59void Polynomial::MakeNTT(void){60 NTT(A, len, DFT), NTT(B, len, DFT);61 for(int i = 0; i <= len; ++i)A[i] = ((ll)A[i] * B[i]) % MOD;62 NTT(A, len, IDFT);63 int mul_inv = kpow(len, MOD - 2);64 for(int i = 0; i <= lena + lenb - 2; ++i)65 printf("%d%c", (ll)A[i] * mul_inv % MOD, i == lena + lenb - 2 ? '\n' : ' ');66}67void Polynomial::Reverse(int* pol){68 int pos[len + 10];69 memset(pos, 0, sizeof(pos));70 for(int i = 0; i < len; ++i){71 pos[i] = pos[i >> 1] >> 1;72 if(i & 1)pos[i] |= len >> 1;73 }74 for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);75}76void Polynomial::NTT(int* pol, int len, bool pat){77 Reverse(pol);78 for(int size = 2; size <= len; size <<= 1){79 int gn = kpow(pat == DFT ? g : inv_g, (MOD - 1) / size);80 for(int* p = pol; p != pol + len; p += size){81 int mid(size >> 1);82 int g(1);83 for(int i = 0; i < mid; ++i, g = ((ll)g * gn) % MOD){84 auto tmp = ((ll)g * p[i + mid]) % MOD;85 p[i + mid] = (p[i] - tmp + MOD) % MOD;86 p[i] = (p[i] + tmp) % MOD;87 }88 }89 }90}91void Polynomial::Init(void){92 lena = read(), lenb = read();93 for(int i = 0; i <= lena; ++i)A[i] = read();94 for(int i = 0; i <= lenb; ++i)B[i] = read();95 len = 1;96 lena++, lenb++;97 while(len < lena + lenb)len <<= 1;98 g = 3;99 inv_g = kpow(g, MOD - 2);100}101
102template<typename T>103inline T read(void){104 T ret(0);105 short flag(1);106 char c = getchar();107 while(c != '-' && !isdigit(c))c = getchar();108 if(c == '-')flag = -1, c = getchar();109 while(isdigit(c)){110 ret *= 10;111 ret += int(c - '0');112 c = getchar();113 }114 ret *= flag;115 return ret;116}合并DFT优化
这个单独再写一个 Blog 吧,戳此进入。
写在后面
写完之后发现似乎依然没有很清晰的弄明白,然后发现有几个Blog写的更清晰易懂
一小时学会快速傅里叶变换(Fast Fourier Transform)
至于几个TODO等以后再慢慢填坑吧
UPD
update-2022_08_10 初稿
update-2022_08_17 改了一下 latex 在 cnblog 里渲染异常的问题( luogu 里还是炸了,以后再改)
update-2022_08_17 修复 latex 在 luogu 里渲染异常的问题
update-2022_08_22 修复 latex 在 cnblog 里仍然存在的渲染异常问题
update-2022_08_22 添加了递归版程序中的 code
update-2022_08_22 进行一些小优化
update-2022_08_22 添加了非循环写法的讲解与 code
update-2022_08_22 添加了 NTT 的讲解与 code
update-2022_08_22 完善了对模意义下单位根的求法
update-2022_08_23 更改标题
update-2022_08_23 添加几个链接
update-2022_08_25 更新标题和链接