COCI2021-2022 Contest2 题解

更好的阅读体验戳此进入

（建议您从上方链接进入我的个人网站查看此 Blog，在 Luogu 中图片会被墙掉，部分 Markdown 也会失效）

原题面链接

Luogu题面

T1 Kaučuk

题意

Kaučuk 程序只有下列三种命令：

• $\mathtt{\text{section}}$$\texttt{section}$：创建新的一级标题，序号从 $1$$1$ 开始标记。
• $\mathtt{\text{subsection}}$$\texttt{subsection}$：创建新的二级标题，序号在每个一级标题的基础上从 $1$$1$ 开始标记。
• $\mathtt{\text{subsubsection}}$$\texttt{subsubsection}$：创建新的三级标题，序号在每个二级标题的基础上从 $1$$1$ 开始标记。

给定 $n$$n$ 组命令及标题名称，输出所有标题序号及其名称。

Examples

Input_1

3

section zivotinje

section boje

section voce

Output_1

1 zivotinje

2 boje

3 voce

Input_2

4

section zivotinje

subsection macke

subsection psi

subsubsection mops

Output_2

1 zivotinje

1.1 macke

1.2 psi

1.2.1 mops

Input_3

1 zivotinje

1.1 macke

1.2 psi

1.2.1 mops

Output_3

1 zivotinje

1.1 psi

2 voce

2.1 ananas

Solution

没什么营养的模拟题。

Code

xxxxxxxxxx
51
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7

8
using namespace std;
9

10
mt19937 rnd(random_device{}());
11
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
12

13
typedef unsigned int uint;
14
typedef unsigned long long unll;
15
typedef long long ll;
16

17
string cmp1 = "section", cmp2 = "subsection", cmp3 = "subsubsection";
18
string title[110];
19
template<typename T = int>
20
inline T read(void);
21

22
int cur1(0), cur2(0), cur3(0);
23

24
int main(){
25
    int N = read();
26
    while(N--){
27
        string cmp, tit;
28
        cin >> cmp >> tit;
29
        if(!cmp1.compare(cmp))cur2 = 0, cur3 = 0, cout << ++cur1 << " " << tit << endl;
30
        else if(!cmp2.compare(cmp))cur3 = 0, cout << cur1 << "." << ++cur2 << " " << tit << endl;
31
        else cout << cur1 << "." << cur2 << "." << ++cur3 << " " << tit << endl;
32
    }
33
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
34
    return 0;
35
}
36

37
template<typename T>
38
inline T read(void){
39
    T ret(0);
40
    short flag(1);
41
    char c = getchar();
42
    while(c != '-' && !isdigit(c))c = getchar();
43
    if(c == '-')flag = -1, c = getchar();
44
    while(isdigit(c)){
45
        ret *= 10;
46
        ret += int(c - '0');
47
        c = getchar();
48
    }
49
    ret *= flag;
50
    return ret;
51
}

T2 Kutije

题意

Matrin 有 n 个箱子的玩具。箱子分别用序号 1,2,3,⋯,n 表示。初始状态下，每个箱子中有一个与箱子编号相同的玩具。

Matrin 邀请了 m 位朋友来家玩玩具。他注意到，每一位朋友在玩完玩具之后，都会将原先位于 i 号箱子内的玩具放入 $p_i$$p_i$ 号箱内。

给定 q 组询问，每次可随意邀请朋友并自由选择顺序，同时每位朋友可以邀请任意多次。问是否存在一种方案，使得 a 号玩具最终被放入 b 号箱子中。

保证 $p_i$$p_i$ 为一个排列。

$1\le n,m\le {10}^3$$1 \le n, m \le 10^3$，$1\le q\le {10}^5$$1 \le q \le 10^5$。

Examples

Input_1

4 1 3 1 2 4 3 1 1 1 2 3 4

Output_1

DA NE DA

Input_2

4 2 4 2 1 3 4 1 2 4 3 2 1 3 4 1 4 2 3

Output_2

DA DA NE NE

Input_3

6 2 2 2 1 4 5 3 6 3 2 4 1 5 6 1 5 6 3

Output_3

DA NE

Solution

依然是一个没什么营养的水题，考虑因为 $p_i$$p_i$ 是序列所以，所以一定会成环，可以当成无向图，十分显然的并查集，就不多赘述了。

搜索，最短路之类的也能过，可以但没必要。

Code

xxxxxxxxxx
61
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7

8
using namespace std;
9

10
mt19937 rnd(random_device{}());
11
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
12

13
typedef unsigned int uint;
14
typedef unsigned long long unll;
15
typedef long long ll;
16

17
class UnionFind{
18
    private:
19
        int fa[1100];
20
    public:
21
        UnionFind(void){for(int i = 0; i <= 1000; ++i)fa[i] = i;}
22
        void Union(int x, int y){fa[y] = x;}
23
        int Find(int x){if(fa[x] == x)return x; return fa[x] = Find(fa[x]);}
24
}UF;
25

26
template<typename T = int>
27
inline T read(void);
28

29
int N, M, Q;
30

31
int main(){
32
    N = read(), M = read(), Q = read();
33
    for(int m = 1; m <= M; ++m){
34
        for(int i = 1; i <= N; ++i){
35
            int tmp = read();
36
            if(UF.Find(i) != UF.Find(tmp))UF.Union(i, tmp);
37
        }
38
    }
39
    while(Q--){
40
        printf("%s\n", UF.Find(read()) == UF.Find(read()) ? "DA" : "NE");
41
    }
42

43
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
44
    return 0;
45
}
46

47
template<typename T>
48
inline T read(void){
49
    T ret(0);
50
    short flag(1);
51
    char c = getchar();
52
    while(c != '-' && !isdigit(c))c = getchar();
53
    if(c == '-')flag = -1, c = getchar();
54
    while(isdigit(c)){
55
        ret *= 10;
56
        ret += int(c - '0');
57
        c = getchar();
58
    }
59
    ret *= flag;
60
    return ret;
61
}

T3 Hiperkocka

题意

(这道题定义了一个 n-dimensional hipercube，但是实际上和这东西没什么关系)

存在一个 $2^n(n\le 16)$$2^n (n \le 16)$ 个节点的图，其中两个节点 $x,y$$x, y$ 连通，当且仅当满足 $x\oplus y=2^{k}k\in \mathbb{N}$$x \oplus y = 2^k \quad k \in \mathbb{N}$。

给定若干棵有 $n+1$$n + 1$ 个节点 $n$$n$ 条边的树，节点用 $0,1,2,\cdots ,n$$0, 1, 2, \cdots, n$ 表示，要求将其放置在图中并对于每棵树都满足如下条件：

• 每棵树上每个节点都与图上节点一一对应。
• 每棵树上的每个节点对应的图上节点互不相同。
• 对于每棵树的边连结的两个节点，对应到图上之后，在图上两个节点仍然是联通的（即对应在图上两个节点的编号按位异或后的值为 $2$$2$ 的整数次幂）。
• 图上的每条边只能对应一个树上的边。

需要你给定一种放置方案，使放置的树尽可能多。

采用 SPJ，可以证明最多能放 $2^{n-1}$$2^{n - 1}$ 棵树，故采用如下方式计算得分：

若放置不合法则获得 $0\mathtt{\text{pts}}$$0 \texttt{pts}$，否则若正确放置了 $k$$k$ 棵树，得分为 $f(k)\times 110\mathtt{\text{pts}}$$f(k) \times 110 \texttt{pts}$，其中：

Examples

Input_1

1 0 1

Output_1

1 0 1

Input_2

2 0 1 1 2

Output_2

2 0 1 3 0 2 3

Input_3

3 0 1 0 2 0 3

Output_3

4 0 1 2 4 3 1 2 7 5 1 4 7 6 2 4 7

Solution

本题的难度基本都在思维和找规律上，代码实现很简单，也并不需要用到任何高级算法和数据结构。

首先我们观察题目里一个很奇怪的条件，$x\oplus y=2^{k}k\in \mathbb{N}$$x \oplus y = 2^k \quad k \in \mathbb{N}$，我们思考对于 $2^k$$2^k$ 的二进制表达，显然有且仅有一个 $1$$1$，而其他位置均为 $0$$0$。我们在考虑运算的性质，异或运算得到 $1$$1$ 的情况则需要两个数这一位置上不同。那么由此我们便不难发现，满足要求的 $x,y$$x, y$ 在二进制上必须有且仅有一位不同。

通过这个性质我们可以进行一些大胆猜想：

假设我们只需要放置一棵树，那么可以考虑采用如下方案：

任意选择一个树上的节点作为根，并对应到图上的任意节点，这里我们考虑令树上的 $0$$0$ 节点映射到图上的 $0$$0$ 节点，记作 $0⟶0$$0 \longrightarrow 0$。

对于树上剩余的点，我们考虑对其进行 DFS，按照其 DFS 序为其分配映射到图上的节点。

为了保证我们映射的节点不会重复，这里我们按照如下方案选点，对于 DFS 序等于 $\xi$$\xi$ 的点，我们考虑使其父节点映射的图上节点对应的第 $\xi$$\xi$ 位进行取反，可以通过对该位进行异或 $1$$1$ 来实现。如果令父亲节点映射到图上的节点为 $ϵ$$\epsilon$ 则可以记作：$\xi ⟶ϵ\oplus (1\times 2^{\xi -1})$$\xi \longrightarrow \epsilon \oplus (1 \times 2^{\xi - 1})$，或写成在搜索过程中写成 dfs(son, cur ^ (1 << (cur++)))。

现在我们就需要扩展到更多的树，注意题目有个要求即每条边只能用一次，那么就需要注意扩展的时候不能使用两次相同图上的父子关系（包括父子之间调换），这里我们可以尝试从一些较小的数找规律。

首先考虑若父亲为 $ϵ$$\epsilon$，其儿子为 $\xi$$\xi$，则将父子关系记作 $ϵ\to \xi$$\epsilon \rightarrow \xi$。

下面我们先找一种特殊情况，如 $n=3$$n = 3$，树为一条 $0\to 1\to 2\to 3$$0 \rightarrow 1 \rightarrow 2 \rightarrow 3$ 的链时，考虑每一种 $0⟶ii\in [0,2^n-1]$$0 \longrightarrow i \quad i \in \left[ 0, 2^n - 1 \right]$（注意此时的 $⟶$$\longrightarrow$ 为长箭头，指的是树与图之间的映射关系，而非父子关系，后文中也以此表示），会有如下可能性：

Tips：这里我们只考虑枚举以树上根节点为 $0$$0$ 映射到图上的任意节点，而不考虑树上的其他根节点的正确性很显然，对于任意一个节点作为根最终形成的结果应该是不变的，可以感性理解一下。

然后我们寻找不合法的解，如果我们贪心地优先保留 $i$$i$ 更小的解，那么下面标注的这些部分显然是重复的不合法的：

观察剩余的合法的解：

不难发现其符合一个规律，即二进制中 $1$$1$ 的数量为偶数个（如果仍未发现可以考虑 $n=4$$n = 4$ 的情况）。

经过验证，显然当树的形态不为一条链的时候该结论仍然成立。

下面我们需要思考如何计算这些扩展出来的节点，显然我们可以每次都进行一次 $\mathtt{\text{DFS}}$$\texttt{DFS}$，时间复杂度大约是 $O(n{2}^n)$$O(n2^n)$，显然可以接受，于是这题就切了...不过我们可以考虑接着找规律（虽然并不能优化复杂度）。

观察刚才得到的合法解中的每一列：

不难发现第一个可能的规律，将 $i=0$$i = 0$ 的情况中每一个数的第 $k$$k$ 位保留不变并将其他位全部取反，枚举 $k$$k$ 便可以得到剩余的情况。但是这真的正确吗？我们可以考虑随意构造一个非链状的树，简单验证后就会发现这个规律假掉了（这里就不写验证过程了，很简单）。

于是我们继续尝试构造规律，可以发现若对于每一个符合要求的 $i(i\ne 0)$$i (i \neq 0)$ 与 $i=0$$i = 0$ 时的每一个数进行异或运算后，得到的结果便是一组新的解，并且经过验证这个规律在其他树的形态仍然是正确的。

至此我们便可以考虑用 dp 思想，$O(2^n)$$O(2^n)$ 预处理出所有合法的 $i$$i$，然后按照我们的算法进行计算，时间复杂度大概是 $O(n{2}^n)$$O(n2^n)$，可以接受。

同时建议对于这种规律题如果有时间，打个对拍验证一下规律的正确性。

Code

xxxxxxxxxx
77
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7

8
using namespace std;
9

10
mt19937 rnd(random_device{}());
11
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
12

13
typedef unsigned int uint;
14
typedef unsigned long long unll;
15
typedef long long ll;
16

17
template<typename T = int>
18
inline T read(void);
19

20
vector < int > vert[110000];
21
int N;
22
int base[110000];
23
bool vis[110000];
24
int cur(0);
25
void dfs(int p, int mapp){
26
    base[p] = mapp;
27
    vis[p] = true;
28
    for(auto i : vert[p]){
29
        if(!vis[i]){
30
            vis[i] = true;
31
            dfs(i, mapp ^ (1 << (cur++)));
32
        }
33
    }
34
}
35
int dp[110000];
36
vector < int > legal;
37
void Init(int N){
38
    int lim = 1 << N;
39
    dp[0] = 0;
40
    for(int i = 1; i <= lim; ++i){
41
        dp[i] = dp[i >> 1] + (i & 1);
42
        if(!(dp[i] & 1))legal.push_back(i);
43
    }
44
}
45
int main(){
46
    N = read();
47
    for(int i = 1; i <= N; ++i){
48
        int f = read(), t = read();
49
        vert[f].push_back(t);
50
        vert[t].push_back(f);
51
    }
52
    dfs(0, 0);
53
    Init(N);
54
    printf("%d\n", (int)legal.size() + 1);
55
    for(int i = 0; i <= N; ++i)printf("%d%c", base[i], i == N ? '\n' : ' ');
56
    for(auto i : legal)
57
        for(int j = 0; j <= N; ++j)
58
            printf("%d%c", base[j] ^ i, j == N ? '\n' : ' ');
59
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
60
    return 0;
61
}
62

63
template<typename T>
64
inline T read(void){
65
    T ret(0);
66
    short flag(1);
67
    char c = getchar();
68
    while(c != '-' && !isdigit(c))c = getchar();
69
    if(c == '-')flag = -1, c = getchar();
70
    while(isdigit(c)){
71
        ret *= 10;
72
        ret += int(c - '0');
73
        c = getchar();
74
    }
75
    ret *= flag;
76
    return ret;
77
}

T4 Magneti

题意

给你 $n$$n$ 个磁铁，第 $i$$i$ 个磁铁都能吸引两侧距离小于 $r_i$$r_i$ 的磁铁，要求将这 $n$$n$ 个磁铁全部放置于 $l$$l$ 个两两距离为 $1$$1$ 的空位中，使得任意两个磁铁都不会被相互吸引，求总方案数，对 ${10}^9+7$$10^9 + 7$ 取模。

• Subtask 1（10 pts）：$r_1=r_2=\cdots =r_n$$r_1=r_2=\cdots=r_n$。
• Subtask 2（20 pts）：$1\le n\le 10$$1 \le n \le 10$。
• Subtask 3（30 pts）：$1\le n\le 30$$1 \le n \le 30$，$n\le l\le 300$$n \le l \le 300$。
• Subtask 4（50 pts）：无特殊限制。

对于 $100\mathrm{\%}$$100\%$ 的数据，$1\le n\le 50$$1 \le n \le 50$，$n\le l\le 10000$$n \le l \le 10000$，$1\le r_i\le l$$1 \le r_i \le l$。

Examples

Input_1

1 10 10

Output_1

10

Input_2

4 4 1 1 1 1

Output_2

24

Input_3

3 4 1 2 1

Output_3

4

Solution

首先我们可以考虑对于有特殊性质的磁铁，当 $r$$r$ 均相等时，我们可以考虑先将所有磁铁挨着放在 $n$$n$ 个空位中的方案，然后将剩下的 $l-n$$l - n$ 个空位，即 $l-n$$l - n$ 个球，可以空闲地分布在 $n$$n$ 个磁铁之间即两侧，也就是 $n+1$$n + 1$ 个盒子，也就是标准球盒问题，用隔板法求解，即：

然后我们可以考虑通过这个性质来思考这道题的思路。

首先我们思考之前的性质，我们先是确定了一部分长度中磁铁如何排列，然后用隔板法计算方案数。所以对于这道题我们的思路也可以去考虑所有的磁铁的合法排列，然后统计总方案数。

我们会发现如果按照每个磁铁输入顺序考虑，并没有什么好的性质，而我们又考虑，对于两个磁铁互相吸引时，显然会优先因为吸引半径更大的磁铁而不合法，所以可以考虑按照吸引半径升序排序，并从每次插入新的磁铁的角度来考虑。

这道题的 $\mathtt{\text{DP}}$$\texttt{DP}$ 还是很显然的，我们可以考虑如何设计状态。

考虑定义一个连通块为一段一定不可能被插入磁铁的区间，且以磁铁开头并以磁铁结尾，显然当两个磁铁，或者更进一步地，两个连通块的吸引区域有重合，或紧挨着，则两个连通块变为同一连通块。

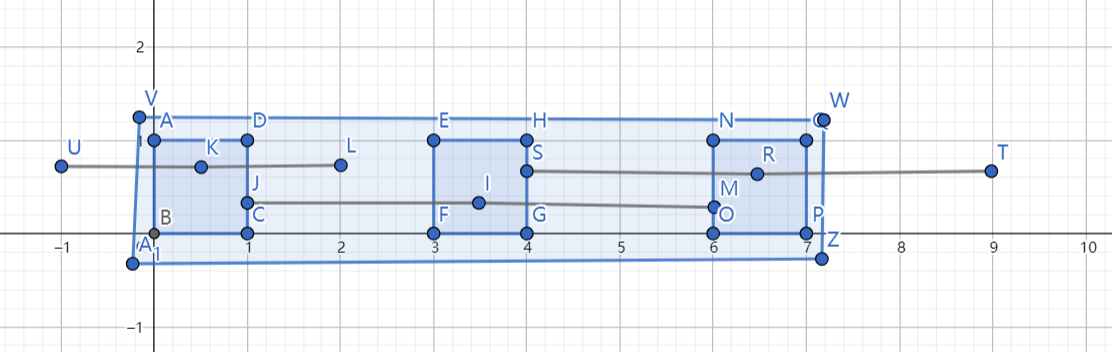
如图，三个正方形为磁铁，线段为磁铁的吸引半径，大长方形即为连通块。

为什么要这样设计连通块？因为我们在每次插入一个新的磁铁的时候都要考虑如何放置，而因为升序的原因，我们只需要考虑新插入的磁铁的吸引半径，所以对于每个连通块左右的吸引半径可以忽略。

可以考虑令 $dp(i,j,k)$$dp(i, j, k)$ 表示已经插入了 $i$$i$ 个磁铁（或正在插入第 $i$$i$ 个磁铁），已经形成了 $j$$j$ 个连通块，占用了 $k$$k$ 个空位的方案数，需要注意我们这里考虑的只是哪些磁铁在同一连通块内的方案数，而未考虑排列顺序，即我们记录的 $\mathtt{\text{DP}}$$\texttt{DP}$ 是组合数。

然后我们考虑转移，对于新插进来的一个磁铁，显然有如下三种可能性，即我们要将 $dp(i,j,k)$$dp(i, j, k)$ 加上如下几种情况的方案数。

upd - Tips: 注意因为我们的目的是求出来排列方案数然后按照隔板法求，所以我们插入一个新的连通块的时候应该去贪心地让新的磁铁尽可能地挨着原来的连通块。

单独形成一个连通块

显然会使连通块多一个，剩余空位少一个，即：

连接在某一个连通块的前端或后端

因为升序排列，所以只考虑我们插入的这个磁铁会占用 $r_i-1+1$$r_i - 1 + 1$ 的空位。

而一共有 $j$$j$ 个连通块可以选择，前端后端均可选择，即：

在两个连通块之间，将两个连通块连接起来

这里需要注意一个点，我们考虑的是磁铁之间的组合而非排列，所以任意两个块之间都可以被连结，且两者之间不同的顺序也是不同的方案。

与第二种情况类似，因为升序排列，只需要考虑插入的这个磁铁，为了连结，会在左右两侧各自占用 $r_i-1$$r_i - 1$ 的空位，自己又会占用 $1$$1$ 的空位，且连通块减少一个，即：

方案的计算

$\mathtt{\text{DP}}$$\texttt{DP}$ 之后我们显然可知，要求的每一个合法方案都应该是连通块的个数为 $1$$1$ 的方案，即：

Code

xxxxxxxxxx
86
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define MOD 1000000007//(int)(1e9 + 7)
8

9
/******************************
10
abbr
11

12
******************************/
13

14
using namespace std;
15

16
mt19937 rnd(random_device{}());
17
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
18

19
typedef unsigned int uint;
20
typedef unsigned long long unll;
21
typedef long long ll;
22

23
ll qpow(ll a, ll b){
24
    ll ret(1), mul(a);
25
    while(b){
26
        if(b & 1)ret = ret * mul % MOD;
27
        b >>= 1;
28
        mul = mul * mul % MOD;
29
    }
30
    return ret;
31
}
32
ll frac[11000], inv[11000];
33
void Init(int N){
34
    frac[0] = 1;
35
    for(int i = 1; i <= N; ++i)frac[i] = frac[i - 1] * i % MOD;
36
    inv[N] = qpow(frac[N], MOD - 2);
37
    for(int i = N - 1; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
38
}
39
ll C(int n, int m){
40
    if(m > n)return 0;
41
    return frac[n] * inv[m] % MOD * inv[n - m] % MOD;
42
}
43
template<typename T = int>
44
inline T read(void);
45

46
int N, L;
47
int r[110];
48
ll dp[55][55][11000];
49
int main(){
50
    N = read(), L = read();
51
    Init(10100);
52
    for(int i = 1; i <= N; ++i)r[i] = read();
53
    sort(r + 1, r + N + 1);
54
    dp[0][0][0] = 1;
55
    for(int i = 1; i <= N; ++i)
56
        for(int j = 1; j <= i; ++j)
57
            for(int k = 1; k <= L; ++k){
58
                dp[i][j][k] = dp[i - 1][j - 1][k - 1];
59
                if(k >= r[i])dp[i][j][k] += dp[i - 1][j][k - r[i]] * j % MOD * 2 % MOD;
60
                if(k >= r[i] * 2 - 1)dp[i][j][k] += dp[i - 1][j + 1][k - r[i] * 2 + 1] * (j + 1) % MOD * (j + 1 - 1) % MOD;
61
                dp[i][j][k] %= MOD;
62
            }
63
    ll ans(0);
64
    for(int i = 1; i <= L; ++i)ans += dp[N][1][i] * C(L - i + 1 + N - 1, N + 1 - 1) % MOD;
65
    printf("%lld\n", ans % MOD);
66
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
67
    return 0;
68
}
69

70

71

72
template<typename T>
73
inline T read(void){
74
    T ret(0);
75
    short flag(1);
76
    char c = getchar();
77
    while(c != '-' && !isdigit(c))c = getchar();
78
    if(c == '-')flag = -1, c = getchar();
79
    while(isdigit(c)){
80
        ret *= 10;
81
        ret += int(c - '0');
82
        c = getchar();
83
    }
84
    ret *= flag;
85
    return ret;
86
}

T5 Osumnjičeni

题意

有 $n$$n$ 个区间，编号为 $1,2,\cdots ,n$$1, 2, \cdots, n$，每次操作可以标记连续一段编号的区间，要求其中的区间互不相交。$q$$q$ 组询问，每次给出一个编号的区间，求出标记这个编号区间内所有区间至少需要多少次。

$1\le n,q\le 2\times {10}^5$$1 \le n, q \le 2 \times 10^5$。

Examples

Input_1

2 1 1 1 1 3 1 1 2 2 1 2

Output_1

1 1 2

Input_2

3 1 1 2 2 3 3 3 1 1 2 3 1 3

Output_2

1 1 1

Input_3

5 1 3 3 3 4 6 2 3 1 1 3 1 4 3 5 1 5

Output_3

3 1 3

Solution

首先有一个很显然的贪心，即当我们某一次标记的区间 $[l,r]$$\left[ l, r \right]$ 的 $l$$l$ 确定之后，为了标记次数尽量少，我们一定要在合法的情况下尽量让标记区间更大，即 $r$$r$ 更大，所以我们自然可以对于 $n$$n$ 个区间维护出每一个 $l$$l$ 对应的最大的 $r$$r$，考虑使用数据结构：

权值线段树 + 单调队列。

不难想到，用单调队列的思想存身高区间，用权值线段树维护，在当前单调队列中所有身高区间值域中，如果插入新的身高区间，会有哪些身高区间因有区间相交而不合法。以此即可 $O(n\log n)$$O(n \log n)$ 处理出每一个 $l$$l$ 对应的最大 $r$$r$。

并且此时我们发现值域过大，并且值域具体的数并不重要，只需要考虑大小关系，所以考虑进行离散化。

于是此时我们便可以发现问题转化为了区间覆盖问题，即CF1175E Minimal Segment Cover。

也就是我们现在有 $n$$n$ 段 $[l,r]$$\left[ l, r \right]$，要求出覆盖 $[l^{\prime },r^{\prime }]$$\left[l', r'\right]$ 至少需要多少段区间。

这里有一个细节需要注意，在我们当前的算法中可能 $l=r$$l = r$，而区间覆盖中是不允许的，所以我们可以考虑把区间改为 $(l,r]$$\left( l, r \right]$，即可很直观地解决。

对于区间覆盖显然就是一个 $O(n\log n)$$O(n \log n)$ 的预处理和 $O(q\log n)$$O(q \log n)$ 的查询，记录从 $i$$i$ 点出发用 $2^j$$2^j$ 条线段最远达到的位置，倍增跑一下就好了，具体可以去看模板题的题解，和这题几乎没区别。

xxxxxxxxxx
123
1
#define _USE_MATH_DEFINES
2
#include <bits/stdc++.h>
3

4
#define PI M_PI
5
#define E M_E
6
#define npt nullptr
7
#define MAXNQ (210000)
8

9
/******************************
10
abbr
11
st => Segment Tree
12
lt => LazyTag
13
gl/gr => global left/right
14
ms => Max Section
15
sec => Section
16
******************************/
17

18
using namespace std;
19

20
mt19937 rnd(random_device{}());
21
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
22

23
typedef unsigned int uint;
24
typedef unsigned long long unll;
25
typedef long long ll;
26

27
int ms;
28
int N, Q;
29

30
class SegTree{
31
    private:
32
        #define LS (p << 1)
33
        #define RS ((p << 1) + 1)
34
        #define MID ((gl + gr) >> 1)
35
        int st[MAXNQ << 3], lt[MAXNQ << 3];
36
    public:
37
        void Pushdown(int p, int gl, int gr){
38
            if(gl == gr)return (void)(lt[p] = 0);
39
            st[LS] += lt[p], st[RS] += lt[p];
40
            lt[LS] += lt[p], lt[RS] += lt[p];
41
            lt[p] = 0;
42
        }
43
        void Modify(int l, int r, int val, int p = 1, int gl = 1, int gr = ms){
44
            // printf("modifying l=%d, r=%d, v=%d, p=%d, gl=%d, gr=%d\n", l, r, val, p, gl, gr);
45
            if(l <= gl && gr <= r){st[p] += val, lt[p] += val; return;}
46
            if(lt[p])Pushdown(p, gl, gr);
47
            if(l <= MID)Modify(l, r, val, LS, gl, MID);
48
            if(MID + 1 <= r)Modify(l, r, val, RS, MID + 1, gr);
49
            st[p] = st[LS] + st[RS];
50
        }
51
        bool Query(int l, int r, int p = 1, int gl = 1, int gr = ms){
52
            // printf("querying l=%d, r=%d p=%d, gl=%d, gr=%d\n", l, r, p, gl, gr);
53
            if(l <= gl && gr <= r)return st[p];
54
            if(lt[p])Pushdown(p, gl, gr);
55
            return ((l <= MID) ? Query(l, r, LS, gl, MID) : false ) | ((MID + 1 <= r) ? Query(l, r, RS, MID + 1, gr) : false); 
56
        }
57
}st;
58

59
template<typename T = int>
60
inline T read(void);
61

62
pair < int, int > sec[MAXNQ];
63
vector < int > values;
64
//1e5 < 2^17
65
int dp[MAXNQ][30];
66

67
int main(){
68
    N = read();
69
    for(int i = 1; i <= N; ++i){
70
        int l = read(), r = read();
71
        sec[i] = make_pair(l, r);
72
        values.push_back(l), values.push_back(r);
73
    }
74
    sort(values.begin(), values.end());
75
    ms = distance(values.begin(), unique(values.begin(), values.end()));
76
    for(int i = 1; i <= N; ++i){
77
        sec[i].first = distance(values.begin(), lower_bound(values.begin(), values.begin() + ms, sec[i].first) + 1);
78
        sec[i].second = distance(values.begin(), lower_bound(values.begin(), values.begin() + ms, sec[i].second) + 1);
79
    }
80
    int cur(1);
81
    for(int i = 1; i <= N; ++i){
82
        while(st.Query(sec[i].first, sec[i].second))
83
            st.Modify(sec[cur].first, sec[cur].second, -1),
84
            dp[cur - 1][0] = i - 1,
85
            ++cur;
86
        st.Modify(sec[i].first, sec[i].second, 1);
87
    }
88
    while(cur <= N + 1)dp[cur - 1][0] = N, ++cur;
89
    for(int j = 1; j <= 17; ++j)
90
        for(int i = 0; i <= N; ++i)
91
            dp[i][j] = dp[dp[i][j - 1]][j - 1];
92
    Q = read();
93
    while(Q--){
94
        int l = read() - 1, r = read();
95
        int ret(0);
96
        for(int dis = 17; dis >= 0; --dis){
97
            if(dp[l][dis] < r){
98
                ret += 1 << dis;
99
                l = dp[l][dis];
100
            }
101
        }
102
        printf("%d\n", ret + 1);
103
    }
104

105
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
106
    return 0;
107
}
108

109
template<typename T>
110
inline T read(void){
111
    T ret(0);
112
    short flag(1);
113
    char c = getchar();
114
    while(c != '-' && !isdigit(c))c = getchar();
115
    if(c == '-')flag = -1, c = getchar();
116
    while(isdigit(c)){
117
        ret *= 10;
118
        ret += int(c - '0');
119
        c = getchar();
120
    }
121
    ret *= flag;
122
    return ret;
123
}

UPD

2022_09_05 完成 T1 - T3 及 T4 一部分

2022_09_06 初稿

2022_09_07 修改了 T3 T4 的一些存在的错误