COCI2021-2022 Contest1 题解
COCI2021-2022 Contest1 题解更好的阅读体验戳此进入原题面链接Luogu题面T1 Ljeto题意ExamplesSolutionT2 Kamenčići题面ExamplesSolutionCodeT3 Logičari题面ExamplesSolution思路找环上边删边状态设计细节处理主函数CodeT4 Set题面(重新翻译了一个新的题面,已经提交到 Luogu)ExamplesSolution性质1性质2性质3性质4性质5FWT 的思路本题如何做?如何推式子?两个小细节CodeT5 Volontiranje题面ExamplesSolutionCodeUPD
更好的阅读体验戳此进入
(建议您从上方链接进入我的个人网站查看此 Blog,在 Luogu 中图片会被墙掉,部分 Markdown 也会失效)
原题面链接
Luogu题面
T1 Ljeto
题意
给你
Examples
Input_1
3
10 1 6
20 1 7
21 8 1
Output_1
250 100
Input_2
3
10 2 5
15 2 6
25 2 5
Output_2
400 0
Input_3
2
10 5 2
11 6 3
Output_3
0 200
Solution
需要注意如果有十秒内连续三次击中,可以加两次
另外需要注意的是在 Luogu 的翻译题面中并没有说明
The numbers
are distinct and are ordered increasingly.
保证了升序输入且不会有相同。
upd - 已向 Luogu 提交翻译错误,题面现已被修改。
将这两点想明白之后这个题就真的是一道入门题了,考虑记录每个人上次击中的时间,直接根据题意模拟即可。
xxxxxxxxxx511
4
8using namespace std;9
10mt19937 rnd(random_device{}());11int rndd(int l, int r){return rnd() % (r - l + 1) + l;}12
13typedef unsigned int uint;14typedef unsigned long long unll;15typedef long long ll;16
17template<typename T = int>18inline T read(void);19
20int as(0), bs(0);21void shot(int n){n <= 4 ? as += 100 : bs += 100;}22void doub(int n){n <= 4 ? as += 50 : bs += 50;}23int lshot[10];24int main(){25 for(int i = 0; i <= 9; ++i)lshot[i] = -114514;26 int N = read();27 for(int i = 1; i <= N; ++i){28 int t = read(), a = read(); (void)read();29 if(t - lshot[a] <= 10)doub(a);30 shot(a);31 lshot[a] = t;32 }33 printf("%d %d\n", as, bs);34 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);35 return 0;36}37template<typename T>38inline T read(void){39 T ret(0);40 short flag(1);41 char c = getchar();42 while(c != '-' && !isdigit(c))c = getchar();43 if(c == '-')flag = -1, c = getchar();44 while(isdigit(c)){45 ret *= 10;46 ret += int(c - '0');47 c = getchar();48 }49 ret *= flag;50 return ret;51}T2 Kamenčići
题面
一行
输出在保证两人均采用最优策略的情况下,谁将会取胜。若
Examples
Input_1
4 1
CCCP
Output_1
DA
Input_2
8 2
PCPPCCCC
Output_2
DA
Input_3
9 1
PPCPPCPPC
Output_3
NE
Solution
先说几个乱搞的做法:
首先观察发现似乎可以贪心,如果一边红色一边蓝色显然最优方案一定是取蓝色的。
对于两边都是红色或者都是蓝色,我有个别的贪心方案但是假掉了,题解里有一个贪心方案是尽量让对方更快碰到红色,也就是找到除头尾外,哪边红色石头更近,或者找哪个蓝色石头更远,按照这个思路似乎可以切掉这道题,不过我认为这个方案正确性并不显然,有可能只是运气好数据比较水。
(贪心+随机化可以过更多点,不过因为是捆测,最后似乎还会是
回到正解,石头个数
可以考虑令
显然对于整个区间的红色石子是由三部分构成:区间内红色 +
考虑用前缀和维护每个区间内的红色石子,我们又已经知道当前这个人取走的数量,那么设转移后的
考虑到对手之间获胜状态相反,所以需要取反。考虑到两人均选择最优方式挑选,所以需要或运算。
于是就会有如下状态转移方程:
此时考虑到边界条件就可以得出最终方程:
考虑到初始化较为复杂,可以考虑
Code
xxxxxxxxxx591
4
8using namespace std;9
10mt19937 rnd(random_device{}());11int rndd(int l, int r){return rnd() % (r - l + 1) + l;}12
13typedef unsigned int uint;14typedef unsigned long long unll;15typedef long long ll;16
17template<typename T = int>18inline T read(void);19
20int N, K;21bool stone[400];22int sum[400];23int dp[400][400][400];24int DFS(int l, int r, int k){25 if(~dp[l][r][k])return dp[l][r][k];26 if(k >= K)return false;27 int k_ = sum[N] - (sum[r] - sum[l - 1]) - k;28 if(k_ >= K)return true;29 return dp[l][r][k] = (!DFS(l + 1, r, k_) | !DFS(l, r - 1, k_));30}31
32int main(){33 memset(dp, -1, sizeof(dp));34 N = read(), K = read();35 for(int i = 1; i <= N; ++i){36 char c = getchar(); while(c != 'C' && c != 'P')c = getchar();37 stone[i] = (c == 'C' ? true : false);38 sum[i] = sum[i - 1] + stone[i];39 }40 printf("%s\n", DFS(1, N, 0) ? "DA" : "NE");41 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);42 return 0;43}44
45template<typename T>46inline T read(void){47 T ret(0);48 short flag(1);49 char c = getchar();50 while(c != '-' && !isdigit(c))c = getchar();51 if(c == '-')flag = -1, c = getchar();52 while(isdigit(c)){53 ret *= 10;54 ret += int(c - '0');55 c = getchar();56 }57 ret *= flag;58 return ret;59}T3 Logičari
题面
对一个基环树进行染色,使每个点有且仅有一个,不包括自身的,与他相连的点被染色,求最少染色数(包括无解情况)。
Examples
Input_1
4
1 2
2 3
3 4
4 1
Output_1
2
Input_2
3
1 2
2 3
3 1
Output_2
-1
Input_3
7
1 2
2 3
3 4
4 5
5 6
6 7
2 4
Output_3
4
Solution
思路
该说不说这题的细节是真的多,改了一下午才过了...
不过这题也挺套路,核心思路考虑把基环树拆开做树上
观察题意,首先考虑如果是普通树上的染色问题,很套路的树上
于是考虑找到环上的任意一个边并将其断开,然后枚举这两个点可能的状态,并在
找环上边
一般有两种方法,一种是维护并查集,当新的边连接的两个节点,是同一颗子树上的时候,要找的就是这个边。
另一种方式更简便一些,
xxxxxxxxxx61void FindLoop(int p, int fa){2 for(auto i = head[p]; i; i = i->nxt){3 if(i->to != fa && vis[i->to]){loop = make_pair(p, i->to); return;}4 if(i->to != fa){vis[i->to] = true; FindLoop(i->to, p);}5 }6}删边
如果用的并查集维护,直接记录下并不将这个边存到树里即可。
如果用的
xxxxxxxxxx191void RemoveLoop(void){2 for(auto i = head[loop.first], lasti = (Edge*)npt; i; lasti = i, i = i->nxt){3 if(i->to == loop.second){4 lasti5 ? lasti->nxt = i->nxt6 : head[loop.first] = i->nxt;7 break;8 }9 }10 for(auto i = head[loop.second], lasti = (Edge*)npt; i; lasti = i, i = i->nxt){11 if(i->to == loop.first){12 lasti13 ? lasti->nxt = i->nxt14 : head[loop.second] = i->nxt;15 break;16 }17 }18 tie(root1, root2) = loop;19}状态设计
考虑在普通的树形
考虑令被染色为
设
因为每个点有且只有一个与之相连的节点会被染色,所以我们可以考虑先假设当前节点所有子节点都不染色,并计算求和,然后分别枚举其每一个子节点,计算如果将该子节点涂色最终需要涂多少点,并取最小值。
但是这题的最大难点我认为就是上面这些过程中合法性的判断,也就是细节的处理。
同时因为状态十分复杂,考虑用
细节处理
首先我们需要考虑,哪些状态是不可能出现的:
- 遍历到某个根节点,但当前状态与根节点已经定下来的状态不同。
- 遍历到某个根节点,父亲节点已被染色,且两个根节点都被染色,导致其中某个根节点,考虑上被临时删除的边之后有两个相连的点被染色。
xxxxxxxxxx61if(2 (currentPosition == root1 && currentStatus != root1Status) ||3 (currentPosition == root2 && currentStatus != root2Status) ||4 (currentPosition == root1 && fatherStatus && root2Status) ||5 (currentPosition == root2 && fatherStatus && root1Status)6)return DEFAULT_DP = INF;然后我们需要考虑,什么时候当前的节点的子节点都不能被染色:
- 父节点已经被染色,即当前节点已经有了一个节点与之相连且被染色。
- 当前节点到了某一个根节点,而另一个根节点已被染色,与
xxxxxxxxxx51if(2 fatherStatus ||3 (currentPosition == root1 && root2Status) ||4 (currentPosition == root2 && root1Status)5) ret = min(ret, sonCost);还有个很重要的点就是我们假设都不染色进行求和操作的时候会爆 int 所以需要在求和时需要开 long long。
主函数
回到我们之前说的,要枚举两个根节点的状态,我们可以考虑令其从其中某个根节点开始遍历,显然会简便很多,显然一共可能有如下四种情况。
xxxxxxxxxx91int ans = min(2 {3 Tintage(root1, 0, 0, 0, 0, -1),4 Tintage(root1, 0, 0, 0, 1, -1),5 Tintage(root1, 1, 0, 1, 0, -1),6 Tintage(root1, 1, 0, 1, 1, -1),7 INF8 }9);Code
xxxxxxxxxx1351
4
10using namespace std;11
12mt19937 rnd(random_device{}());13int rndd(int l, int r){return rnd() % (r - l + 1) + l;}14
15typedef unsigned int uint;16typedef unsigned long long unll;17typedef long long ll;18
19template<typename T = int>20inline T read(void);21
22int N;23bool vis[110000];24pair < int, int >/*from, to*/ loop;25int root1, root2;26
27struct Edge{28 Edge* nxt;29 int to;30 void* operator new(size_t);31 Edge(Edge* nxt, int to):nxt(nxt), to(to){;}32 Edge(void) = default;33}eData[210000];34void* Edge::operator new(size_t){static Edge* P = eData; return ++P;}35
36Edge* head[110000];37int dp[110000][2][2][2][2]; /*CurrentPosition, CurrentStatus, FatherStatus, Root1Status, Root2Status*/38
39void FindLoop(int = 1, int = -1);40void RemoveLoop(void);41int Tintage(int, bool, bool, bool, bool, int);42
43int main(){44 memset(dp, -1, sizeof(dp));45 N = read();46 for(int i = 1; i <= N; ++i){47 int from = read(), to = read();48 head[from] = new Edge(head[from], to);49 head[to] = new Edge(head[to], from);50 }51 FindLoop();52 RemoveLoop();53 int ans = min(54 {55 Tintage(root1, 0, 0, 0, 0, -1),56 Tintage(root1, 0, 0, 0, 1, -1),57 Tintage(root1, 1, 0, 1, 0, -1),58 Tintage(root1, 1, 0, 1, 1, -1),59 INF60 }61 );62 printf("%d\n", ans == INF ? -1 : ans);63 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);64 return 0;65}66int Tintage(int currentPosition, bool currentStatus, bool fatherStatus, bool root1Status, bool root2Status, int fatherPosition){67 if(~DEFAULT_DP)return DEFAULT_DP;68 if(69 (currentPosition == root1 && currentStatus != root1Status) ||70 (currentPosition == root2 && currentStatus != root2Status) ||71 (currentPosition == root1 && fatherStatus && root2Status) ||72 (currentPosition == root2 && fatherStatus && root1Status)73 )return DEFAULT_DP = INF;74 ll sonCost(currentStatus);75 for(auto i = head[currentPosition]; i; i = i->nxt)76 if(i->to != fatherPosition)77 sonCost += Tintage(i->to, false, currentStatus, root1Status, root2Status, currentPosition);78 ll ret(INF);79 if(80 fatherStatus ||81 (currentPosition == root1 && root2Status) ||82 (currentPosition == root2 && root1Status)83 ) ret = min(ret, sonCost);84 else 85 for(auto i = head[currentPosition]; i; i = i->nxt)86 if(i->to != fatherPosition)87 ret = min({88 ret,89 (ll)INF,90 sonCost - Tintage(i->to, false, currentStatus, root1Status, root2Status, currentPosition)91 + Tintage(i->to, true, currentStatus, root1Status, root2Status, currentPosition)92 });93 return DEFAULT_DP = ret;94}95void RemoveLoop(void){96 for(auto i = head[loop.first], lasti = (Edge*)npt; i; lasti = i, i = i->nxt){97 if(i->to == loop.second){98 lasti99 ? lasti->nxt = i->nxt100 : head[loop.first] = i->nxt;101 break;102 }103 }104 for(auto i = head[loop.second], lasti = (Edge*)npt; i; lasti = i, i = i->nxt){105 if(i->to == loop.first){106 lasti107 ? lasti->nxt = i->nxt108 : head[loop.second] = i->nxt;109 break;110 }111 }112 tie(root1, root2) = loop;113}114void FindLoop(int p, int fa){115 for(auto i = head[p]; i; i = i->nxt){116 if(i->to != fa && vis[i->to]){loop = make_pair(p, i->to); return;}117 if(i->to != fa){vis[i->to] = true; FindLoop(i->to, p);}118 }119}120
121template<typename T>122inline T read(void){123 T ret(0);124 short flag(1);125 char c = getchar();126 while(c != '-' && !isdigit(c))c = getchar();127 if(c == '-')flag = -1, c = getchar();128 while(isdigit(c)){129 ret *= 10;130 ret += int(c - '0');131 c = getchar();132 }133 ret *= flag;134 return ret;135}T4 Set
题目背景
在知名游戏
中,存在着一些数字、形状、颜色等不同的卡片,玩家的目标是确定一个存在的 (即卡片的三元组,也就是三张卡片构成的组合),使其符合特定的要求。 和 很快就对这个游戏感到无趣,并对其进行了加强。 题目描述
在本题中,定义每张卡片代表着一个仅由
构成的长度为 的序列,共有 张卡片,卡片之间是无序的。 定义一个
表示,当且仅当一个无序的 其中的三个序列的每一位均相同或各不相同,用原文中的话就是 或 ,更严谨地表示,我们令这三个序列为 ,则一定满足如下条件:
,满足 或 例如
便满足 位均相同, 位各不相同。 给你这些序列,求可以组成多少种本质不同的
。 输入格式
第一行为两个整数正整数
。 接下来
行中每一行包含一个仅由 构成的长度为 的序列,代表着一张卡片。 保证每张卡片上的序列不同。
输出格式
仅一行一个整数,表示可以组成的本质不同的
的数量。 说明 / 提示
样例 3 解释
可以组成的两个
分别为 和 。 数据范围
对于全部数据,满足
, 互不相同且满足 。
Subtask 特殊限制 分数 1 10 2 30 3 无特殊限制 70
题面(重新翻译了一个新的题面,已经提交到 Luogu)
Examples
Input_1
3 4
1123
1322
1221
Output_1
1
Input_2
2 2
11
22
Output_2
0
Input_3
5 3
111
222
333
123
132
Output_3
2
Solution
需要用到很多
观察题意,发现对于每个
思考这个规律有什么性质
性质1
显然设这三个数为
证明:这么显然还需要证明吗。
性质2
当这个
证明:一共就三个可能的数,这个也很显然吧
然后我们发现这两个性质无法继续向下推,于是我们考虑假设存在一个自洽的代数系统
同时我们考虑定义一元运算符
此时我们会发现更多的性质:
性质3
一个数与其自身进行两次
证明:根据
性质4
运算
证明:显然成立。
性质5
对于性质1,由新的定义可以转化为如下式子:
也就是:
此时根据这些性质,如果我们令
则显然
(注意这里并不是本质不同,所以也可以理解为
这里我们定义序列
需要注意下标
存在与否指的是是否在题目给出的
容易看出会有如下式子:
当然这个式子也可以记作:
而我们需要的便是这个式子的常数项
仔细观察一般的式子,这像什么?显然是多项式的各种快速变换!或者进一步说,很像
FWT(快速沃尔什变换)一般用于处理形如如下式子的卷积:
此处的
一般为 &, |, ^, 也就是 。
发现我们当前的式子很像
FWT 的思路
与大多数多项式快速变换的思路一样,我们的目的都是找到一种变换,对于
我们需要让这个变换满足以下性质:
且:
对于不同的运算都有着与之对应的不同的变换方式,我们的目的就是要找到一种优秀的变换并快速地进行变换。
这里额外说一下对于多项式约定俗成的几种运算表示什么,相信你们一定都知道
(主要因为我最开始做这道题的时候有的符号理解错了)这里我们假设
最高次为 次, 最高次为 次。 令
。
本题如何做?
通过上面的信息显然我们便可确定本题的核心:找出在代数系统
从哪入手呢?观察对于常用的三个运算的
如何推式子?
再次观察我们定义的这个二元运算符
题外话:写到这里突然发现我好像推不出来这个式子,于是决定先去把
的坑填了...
我们要求的可以理解为是以下的式子:
用和
我们需要保证对于转移矩阵
观察运算的性质,和三进制下的异或运算性质较为相似,可以考虑尝试范德蒙德矩阵:
可以化简为:
逆矩阵同理容易得出为:
可以化简为:
显然我们可以算出:
且:
到此我们便可以求出来最终的结果了。
这里还有两个小细节需要注意:
两个小细节
首先我们在做完
然后还需要注意当我们算出来常数项之后,并不能直接输出,观察一下性质 3:
在运算的时候我们显然会把
并且,我们在运算的时候求的是不同,而非本质不同,也就是算的是排列,而我们要求的是组合,所以最后除一个
综上所述,我们将常数项算出来后最终答案就是
至此,这道卡了我两天多的题,终于结束了。
(记得开 long long)
Code
xxxxxxxxxx901
4
9using namespace std;10
11mt19937 rnd(random_device{}());12int rndd(int l, int r){return rnd() % (r - l + 1) + l;}13
14typedef unsigned int uint;15typedef unsigned long long unll;16typedef long long ll;17
18template<typename T = int>19inline T read(void);20inline int read3(void);21
22int N, M;23// 3^12 = 53144124comp poly[1100000];25comp omega(-0.5, 0.5 * sqrt(3));26comp omega2(conj(omega));27enum pattern{IFWT = 0, _FWT};28void FWT(comp*, int, pattern);29
30int main(){31 N = read(), M = read();32 for(int i = 1; i <= N; ++i)poly[read3()].real(1.0);33 int lim(1), cnt(0);34 while(cnt++ < M)lim *= 3;35 FWT(poly, lim, _FWT);36 for(int i = 0; i < lim; ++i)poly[i] = poly[i] * poly[i] * poly[i];37 FWT(poly, lim, IFWT);38 ll ans = (poly[0].real() / (long double)lim) + 0.5;39 printf("%lld\n", (ans - N) / 6);40 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);41 return 0;42}43void FWT(comp* poly, int lim, pattern pat){44 for(int len = 1; len < lim; len *= 3)45 for(int px = 0; px < lim; px += 3 * len)46 for(int p = 0; p < len; ++p){47 int pos1(px + p + len * 0),48 pos2(px + p + len * 1),49 pos3(px + p + len * 2);50 comp pol1 = poly[pos1];51 comp pol2 = poly[pos2];52 comp pol3 = poly[pos3];53 if(pat == _FWT){54 poly[pos1] = pol1 + pol2 + pol3;55 poly[pos2] = pol1 + pol2 * omega + pol3 * omega2;56 poly[pos3] = pol1 + pol2 * omega2 + pol3 * omega;57 }else{58 poly[pos1] = pol1 + pol2 + pol3;59 poly[pos2] = pol1 + pol2 * omega2 + pol3 * omega;60 poly[pos3] = pol1 + pol2 * omega + pol3 * omega2;61 }62 }63}64
65inline int read3(void){66 int ret(0);67 char c = getchar();68 while(!isdigit(c))c = getchar();69 while(isdigit(c)){70 ret *= 3;71 ret += int(c - '0' - 1);72 c = getchar();73 }74 return ret;75}76template<typename T>77inline T read(void){78 T ret(0);79 short flag(1);80 char c = getchar();81 while(c != '-' && !isdigit(c))c = getchar();82 if(c == '-')flag = -1, c = getchar();83 while(isdigit(c)){84 ret *= 10;85 ret += int(c - '0');86 c = getchar();87 }88 ret *= flag;89 return ret;90}T5 Volontiranje
这题比 T4 简单多了。
题面
给定一个长度为 (是的就这么简洁)
输出个数,长度,并输出每一个最长上升子序列。
Examples
Input_1
3
1 2 3
Output_1
1 3
1 2 3
Input_2
4
4 3 2 1
Output_2
4 1
1
2
3
4
Input_3
7
2 1 6 5 7 3 4
Output_3
2 3
1 3 5
2 6 7
Solution
考虑求 LIS 的长度直接 lower_bound 求。
而对于有哪些 LIS,我们则需要找到其中的一些性质,考虑将每个数的下标作为
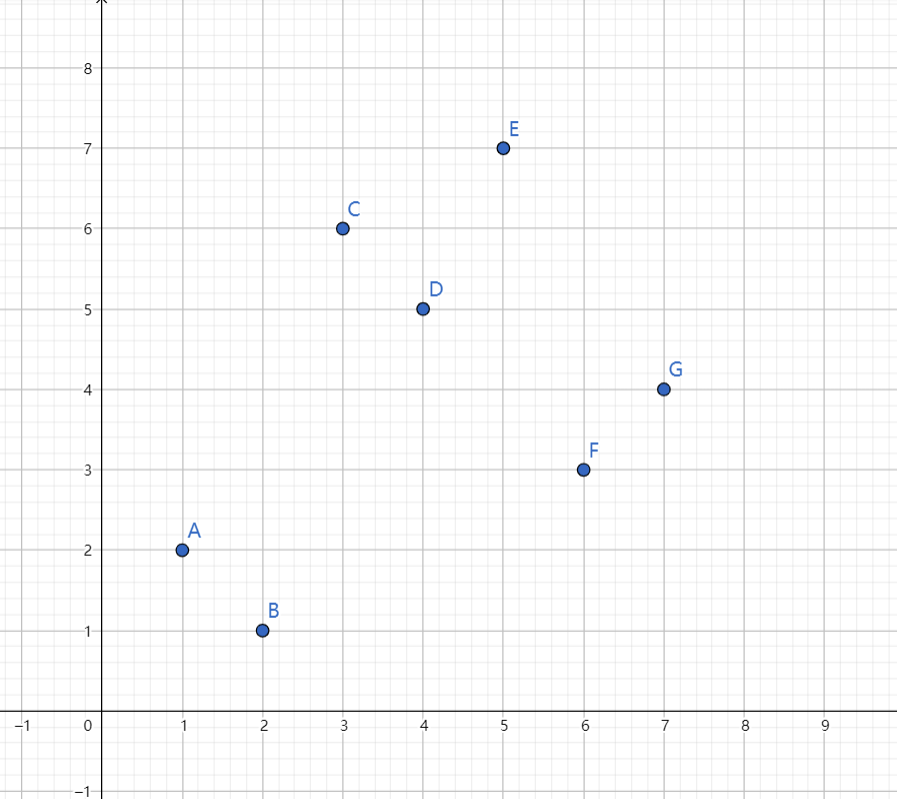
观察这个奇怪的图形我们可以考虑从
也就是如下:
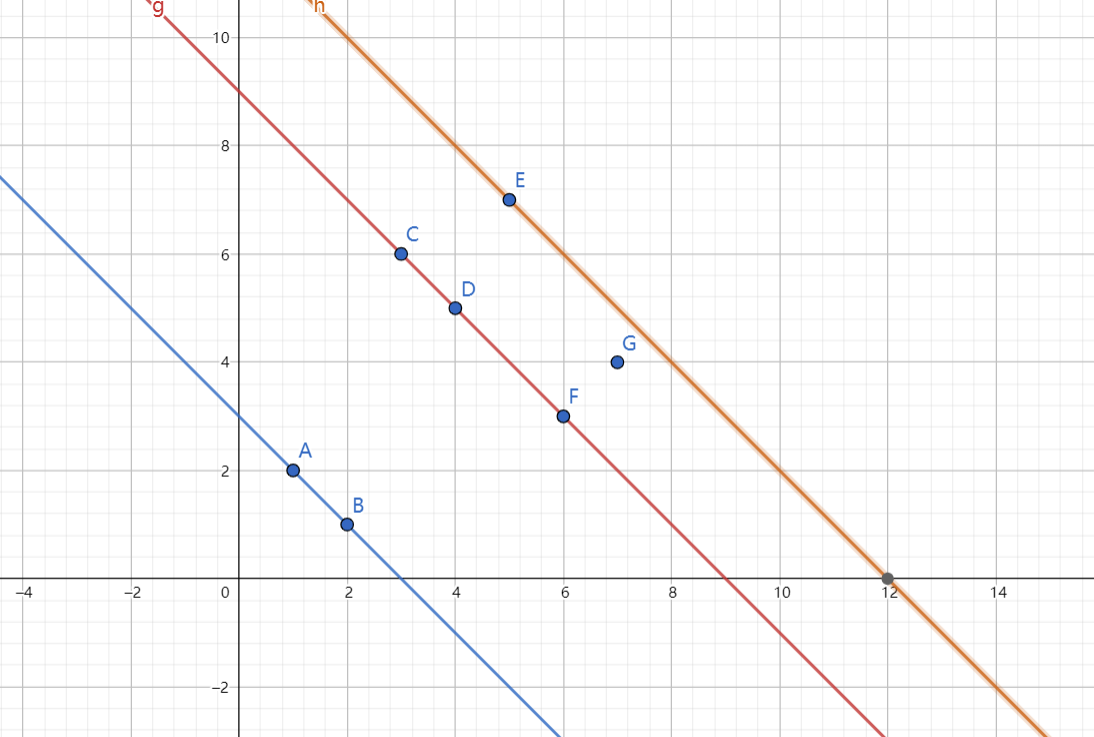
注意这里的层级划分是左下开右上闭的。
于是我们便可以发现,对于每一个 LIS 都应该是从每一个层级中选择一个点并且符合,下一层级的点符合在当前点的右上。
这里我们考虑如何分层,考虑当我们计算 LIS 时,一般用的状态是,以当前点为结尾的 LIS 长度,我们观察发现,第一层级里,
于是我们便可以发现按照
让后我们考虑如何选择每一层级的点,这里我们有一个结论,对于每一层级优先选择纵横坐标,也就是下标更低的未选择过的点一定是更优的,这个正确性可以去举例理解一下,如果对于上图的情况,连结
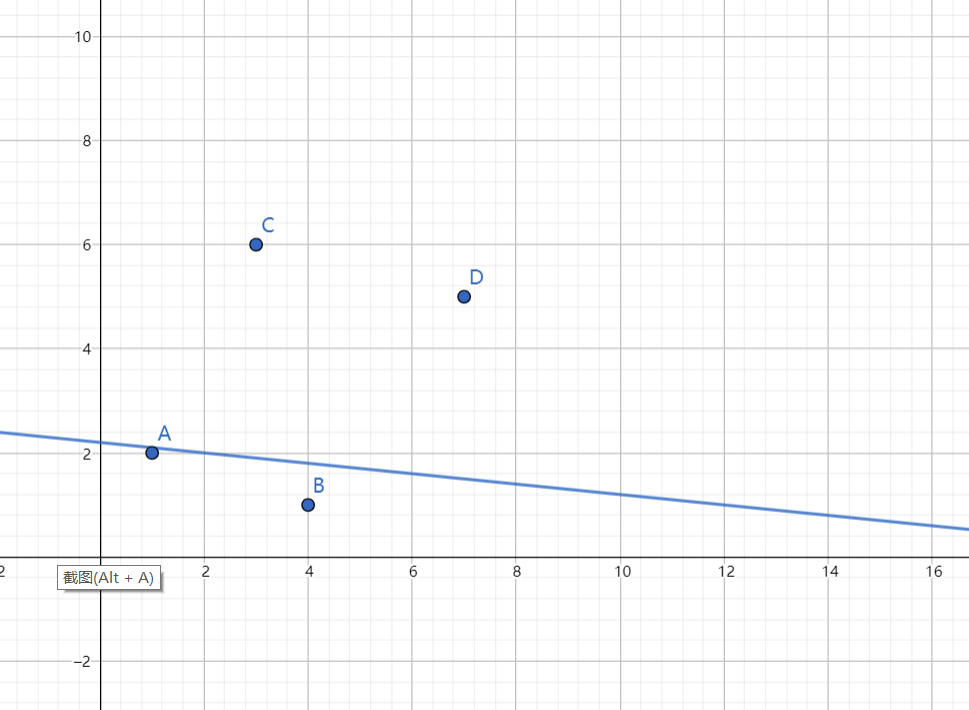
(这里为了方便表述省略了一些点)
显然层级划分的线大概是这样,这个时候如果我们对于
至此我们的推导已经结束,可以进行实现了。
Code
xxxxxxxxxx901
4
8/******************************9abbr10
11******************************/12
13using namespace std;14
15mt19937 rnd(random_device{}());16int rndd(int l, int r){return rnd() % (r - l + 1) + l;}17
18typedef unsigned int uint;19typedef unsigned long long unll;20typedef long long ll;21
22
23
24template<typename T = int>25inline T read(void);26
27vector < int > LISv;28pair < int, int > LIS[1100000];29int N;30vector < int > current;31vector < int > tier[1100000];32int arr[1100000];33vector < vector < int > > anss;34int main(){35 N = read();36 for(int i = 1; i <= N; ++i){37 arr[i] = read();38 if(LISv.empty() || LISv.back() < arr[i])LISv.push_back(arr[i]), tier[(int)LISv.size()].push_back(i);39 else{40 auto pos = lower_bound(LISv.begin(), LISv.end(), arr[i]);41 int len = distance(LISv.begin(), pos) + 1;42 *pos = arr[i];43 tier[len].push_back(i);44 }45 }46 int maxLen = (int)LISv.size();47 for(int i = 1; i <= maxLen; ++i)48 reverse(tier[i].begin(), tier[i].end());49 while(true){50 if(current.empty()){51 if(tier[1].empty())break;52 current.push_back(tier[1].back());53 tier[1].pop_back();54 }else if((int)current.size() == maxLen){55 anss.push_back(current);56 current.clear();57 }else{58 int pos = current.size() + 1;59 int last = current.back();60 while(!tier[pos].empty() && tier[pos].back() < last)tier[pos].pop_back();61 if(tier[pos].empty() || arr[tier[pos].back()] < arr[last])current.pop_back();62 else current.push_back(tier[pos].back()), tier[pos].pop_back();63 }64 }65 printf("%d %d\n", (int)anss.size(), maxLen);66 for(auto i : anss){67 for(auto j : i)printf("%d ", j);68 printf("\n");69 }70 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);71 return 0;72}73
74
75
76template<typename T>77inline T read(void){78 T ret(0);79 short flag(1);80 char c = getchar();81 while(c != '-' && !isdigit(c))c = getchar();82 if(c == '-')flag = -1, c = getchar();83 while(isdigit(c)){84 ret *= 10;85 ret += int(c - '0');86 c = getchar();87 }88 ret *= flag;89 return ret;90}UPD
update-2022_08_30 T1-T3
update-2022_09_01 完成一部分的 T4
update-2022_09_02 T4 肝完
update-2022_09_04 初稿
update-2022_09_04 发现 T4 之前算法假掉了,修改了一下
update-2022_09_06 完善 latex 以符合 Luogu 题解要求