AtCoder Beginner Contest 248 Solution
AtCoder Beginner Contest 248 Solution更好的阅读体验戳此进入题面链接题面 Luogu 链接[ABC248A] Lacked Number题面SolutionCode[ABC248B] Slimes题面SolutionCode[ABC248C] Dice Sum题面SolutionCode[ABC248D] Range Count Query题面SolutionCode[ABC248E] K-colinear Line题面SolutionCode[ABC248F] Keep Connect题面SolutionCode[ABC248G] GCD cost on the tree题面SolutionCode[ABC248Ex] Beautiful Subsequences题面SolutionCodeUPD
更好的阅读体验戳此进入
题面链接
题面 Luogu 链接
[ABC248A] Lacked Number
题面
给定字符集为 0-9 数字的字符串,求字符集中没有在字符串中出现的唯一数字。
Solution
语法题。
Code
xxxxxxxxxx521
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22template< typename T = int >23inline T read(void);24
25bool vis[10];26
27int main(){28 for(int i = 1; i <= 9; ++i){29 char c = getchar();30 while(!isdigit(c))c = getchar();31 vis[c - '0'] = true;32 }for(int i = 0; i <= 9; ++i)if(!vis[i])printf("%d\n", i), exit(0);33
34 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);35 return 0;36}37
38template < typename T >39inline T read(void){40 T ret(0);41 int flag(1);42 char c = getchar();43 while(c != '-' && !isdigit(c))c = getchar();44 if(c == '-')flag = -1, c = getchar();45 while(isdigit(c)){46 ret *= 10;47 ret += int(c - '0');48 c = getchar();49 }50 ret *= flag;51 return ret;52}[ABC248B] Slimes
题面
给定
Solution
语法题,数据范围不大所以直接浮点数搞一下
Code
xxxxxxxxxx471
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22template< typename T = int >23inline T read(void);24
25int main(){26 int A = read(), B = read(), K = read();27 int ans = (int)ceill(log((ld)B / (ld)A) / log((ld)K));28 printf("%d\n", ans);29 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);30 return 0;31}32
33template < typename T >34inline T read(void){35 T ret(0);36 int flag(1);37 char c = getchar();38 while(c != '-' && !isdigit(c))c = getchar();39 if(c == '-')flag = -1, c = getchar();40 while(isdigit(c)){41 ret *= 10;42 ret += int(c - '0');43 c = getchar();44 }45 ret *= flag;46 return ret;47}[ABC248C] Dice Sum
题面
给定
Solution
数据范围太小,写一个
Code
xxxxxxxxxx591
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22
24template< typename T = int >25inline T read(void);26
27int N, M, K;28ll dp[60][3000];29
30int main(){31 N = read(), M = read(), K = read();32 dp[0][0] = 1;33 for(int i = 1; i <= N; ++i)34 for(int j = 1; j <= K; ++j)35 for(int lst = 1; lst <= M; ++lst)36 if(j - lst >= 0)37 (dp[i][j] += dp[i - 1][j - lst]) %= MOD;38 ll ans(0);39 for(int i = 0; i <= K; ++i)(ans += dp[N][i]) %= MOD;40 printf("%lld\n", ans);41 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);42 return 0;43}44
45template < typename T >46inline T read(void){47 T ret(0);48 int flag(1);49 char c = getchar();50 while(c != '-' && !isdigit(c))c = getchar();51 if(c == '-')flag = -1, c = getchar();52 while(isdigit(c)){53 ret *= 10;54 ret += int(c - '0');55 c = getchar();56 }57 ret *= flag;58 return ret;59}[ABC248D] Range Count Query
题面
给定序列
Solution
值域较小,每个数维护一个出现位置的 basic_string,每次在里面二分两次查左右端点调用一下 distance() 即可。
Code
xxxxxxxxxx541
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22template< typename T = int >23inline T read(void);24
25int N, Q;26basic_string < int > pos[210000];27
28int main(){29 N = read();30 for(int i = 1; i <= N; ++i)pos[read()] += i;31 Q = read();32 while(Q--){33 int l = read(), r = read(), x = read();34 printf("%d\n", (int)distance(lower_bound(pos[x].begin(), pos[x].end(), l), upper_bound(pos[x].begin(), pos[x].end(), r)));35 }36 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);37 return 0;38}39
40template < typename T >41inline T read(void){42 T ret(0);43 int flag(1);44 char c = getchar();45 while(c != '-' && !isdigit(c))c = getchar();46 if(c == '-')flag = -1, c = getchar();47 while(isdigit(c)){48 ret *= 10;49 ret += int(c - '0');50 c = getchar();51 }52 ret *= flag;53 return ret;54}[ABC248E] K-colinear Line
题面
给一堆点问有多少条直线至少经过了
Solution
数据范围较小,随便枚举一下然后判个重即可。
Code
xxxxxxxxxx681
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22
24template< typename T = int >25inline T read(void);26
27int N, K;28bool vis[310][310];29struct Coord{int x, y;}p[310];30int ans(0);31bool Check(Coord a, Coord b, Coord c){32 // return (abs((double)(b.y - a.y) / (double)(b.x - a.x) - (double)(c.y - b.y) / (double)(c.x - b.x)) <= EPS);33 return ((ll)(b.y - a.y) * (c.x - b.x) == (ll)(c.y - b.y) * (b.x - a.x));34}35
36int main(){37 N = read(), K = read();38 if(K == 1)printf("Infinity\n"), exit(0);39 for(int i = 1; i <= N; ++i)p[i].x = read(), p[i].y = read();40 for(int i = 1; i <= N; ++i)41 for(int j = i + 1; j <= N; ++j)42 if(!vis[i][j]){43 basic_string < int > pts; pts += {i, j};44 for(int k = 1; k <= N; ++k)45 if(k != i && k != j && Check(p[i], p[j], p[k]))pts += k;46 for(auto u : pts)for(auto v : pts)vis[u][v] = true;47 if((int)pts.size() >= K)++ans;48 }49 printf("%d\n", ans);50 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);51 return 0;52}53
54template < typename T >55inline T read(void){56 T ret(0);57 int flag(1);58 char c = getchar();59 while(c != '-' && !isdigit(c))c = getchar();60 if(c == '-')flag = -1, c = getchar();61 while(isdigit(c)){62 ret *= 10;63 ret += int(c - '0');64 c = getchar();65 }66 ret *= flag;67 return ret;68}[ABC248F] Keep Connect
题面
给定
Solution
这种题 DP 很显然,考虑设状态
具体地,对于
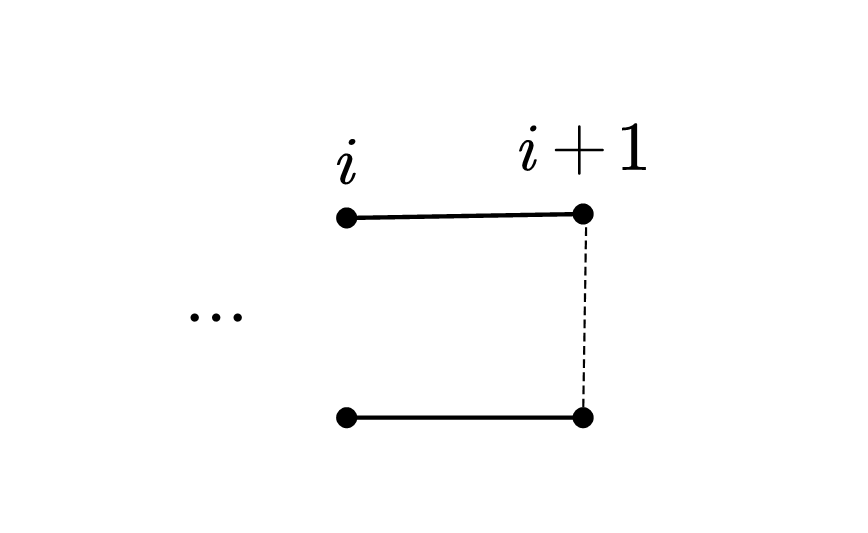
对于
同时注意

边界可以是
Code
xxxxxxxxxx581
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22template< typename T = int >23inline T read(void);24
25int N; int MOD;26int dp[3100][3100][2];27
28int main(){29 N = read(), MOD = read();30 dp[1][0][1] = dp[1][1][0] = 1;31 for(int i = 1; i <= N - 1; ++i)32 for(int j = 0; j <= N - 1; ++j)33 dp[i + 1][j + 1][0] = ((ll)dp[i + 1][j + 1][0] + dp[i][j][0]) % MOD,34 dp[i + 1][j][1] = ((ll)dp[i + 1][j][1] + dp[i][j][0]) % MOD,35 dp[i + 1][j + 1][1] = ((ll)dp[i + 1][j + 1][1] + dp[i][j][1] * 2ll) % MOD,36 dp[i + 1][j][1] = ((ll)dp[i + 1][j][1] + dp[i][j][1]) % MOD,37 dp[i + 1][j + 2][0] = ((ll)dp[i + 1][j + 2][0] + dp[i][j][1] * 2ll) % MOD,38 dp[i + 1][j + 1][1] = ((ll)dp[i + 1][j + 1][1] + dp[i][j][1]) % MOD;39 for(int i = 1; i <= N - 1; ++i)printf("%d%c", dp[N][i][1], i == N - 1 ? '\n' : ' ');40 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);41 return 0;42}43
44template < typename T >45inline T read(void){46 T ret(0);47 int flag(1);48 char c = getchar();49 while(c != '-' && !isdigit(c))c = getchar();50 if(c == '-')flag = -1, c = getchar();51 while(isdigit(c)){52 ret *= 10;53 ret += int(c - '0');54 c = getchar();55 }56 ret *= flag;57 return ret;58}[ABC248G] GCD cost on the tree
题面
给定一颗树有
Solution
考虑枚举每个子树,无脑搜索所有路径,用 map 存储对于每个路径上的
Code
xxxxxxxxxx1041
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22
24template< typename T = int >25inline T read(void);26
27struct Edge{28 Edge* nxt;29 int to;30 OPNEW;31}ed[210000];32ROPNEW(ed);33Edge* head[110000];34
35int N;36ll ans(0);37int a[110000];38struct Paths{39 ll sum, cnt;40 friend const Paths operator + (const Paths &a, const Paths &b){41 return Paths{(a.sum + b.sum) % MOD, (a.cnt + b.cnt) % MOD};42 }43 friend Paths operator += (Paths &origin, const Paths &add){44 return origin = origin + add;45 }46};47
48ll Cal(const map < int, Paths > &a, const map < int, Paths > &b){49 ll ret(0);50 for(auto mpa : a)for(auto mpb : b)51 (ret += (ll)__gcd(mpa.first, mpb.first) * (52 mpa.second.sum * mpb.second.cnt % MOD +53 mpa.second.cnt * mpb.second.sum % MOD +54 mpa.second.cnt * mpb.second.cnt % MOD55 )) %= MOD;56 return ret;57}58auto Extend(const map < int, Paths > &origin, int val){59 map < int, Paths > ret;60 for(auto mp : origin)ret[__gcd(mp.first, val)] += Paths{mp.second.sum + mp.second.cnt, mp.second.cnt};61 return ret;62}63void Union(map < int, Paths > &origin, const map < int, Paths > add){64 for(auto mp : add)origin[mp.first] += mp.second;65}66map < int, Paths > dfs(int p = 1, int fa = 0){67 map < int, Paths > ret;68 ret.insert({a[p], Paths{0, 1}});69 for(auto i = head[p]; i; i = i->nxt){70 if(SON == fa)continue;71 auto son = Extend(dfs(SON, p), a[p]);72 (ans += Cal(ret, son)) %= MOD;73 Union(ret, son);74 }return ret;75}76
77int main(){78 N = read();79 for(int i = 1; i <= N; ++i)a[i] = read();80 for(int i = 1; i <= N - 1; ++i){81 int s = read(), t = read();82 head[s] = new Edge{head[s], t};83 head[t] = new Edge{head[t], s};84 }dfs();85 printf("%lld\n", ans);86 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);87 return 0;88}89
90template < typename T >91inline T read(void){92 T ret(0);93 int flag(1);94 char c = getchar();95 while(c != '-' && !isdigit(c))c = getchar();96 if(c == '-')flag = -1, c = getchar();97 while(isdigit(c)){98 ret *= 10;99 ret += int(c - '0');100 c = getchar();101 }102 ret *= flag;103 return ret;104}[ABC248Ex] Beautiful Subsequences
题面
给定排列
Solution
首先为了方便我们令
于是到此问题可转化为,求区间最大值最小值,然后再求区间等于
然后考虑如何维护区间等于 basic_string < pair < int, int > >,存储对应值有多少个,合并的时候直接把两个加起来即可,然后去个重。同时此时查询的时候可以不用枚举
Code
xxxxxxxxxx1341
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22
24template< typename T = int >25inline T read(void);26
27int N, K;28int val[MAXN];29
30struct MyPair{31 int first, second;32 friend const bool operator < (const MyPair &a, const MyPair &b){33 return a.first == b.first ? a.second < b.second : a.first < b.first;34 }35};36
37struct Node{38 basic_string < MyPair/*val, cnt*/ > vals;39 int lz;40 Node operator = (const Node &b){41 this->vals = b.vals;42 this->lz = b.lz;43 return *this;44 }45 friend const Node operator + (const Node &a, const Node &b){46 Node ret{a.vals + b.vals, 0};47 sort(ret.vals.begin(), ret.vals.end());48 for(auto it = ret.vals.begin(); next(it) != ret.vals.end();)49 if(it->first == next(it)->first)next(it)->second += it->second, it = ret.vals.erase(it);50 else advance(it, 1);51 return ret;52 }53 friend Node operator += (Node &a, const int &val){54 for(auto &nod : a.vals)nod.first += val;55 a.lz += val;56 return a;57 }58};59class SegTree{60private:61 Node tr[MAXN << 2];62 63 64 65public:66 void Pushup(int p){tr[p] = tr[LS] + tr[RS];}67 void Pushdown(int p){68 if(!tr[p].lz)return;69 tr[LS].lz = tr[RS].lz = tr[p].lz;70 tr[LS] += tr[p].lz, tr[RS] += tr[p].lz;71 tr[p].lz = 0;72 }73 void Build(int p = 1, int gl = 1, int gr = N){74 if(gl == gr)return tr[p].vals += {gl = gr, 1}, void();75 Build(LS, gl, MID), Build(RS, MID + 1, gr);76 Pushup(p);77 }78 void Modify(int l, int r, int val, int p = 1, int gl = 1, int gr = N){79 if(l <= gl && gr <= r)return tr[p] += val, void();80 Pushdown(p);81 if(l <= MID)Modify(l, r, val, LS, gl, MID);82 if(r >= MID + 1)Modify(l, r, val, RS, MID + 1, gr);83 Pushup(p);84 }85 Node Query(int l, int r, int p = 1, int gl = 1, int gr = N){86 if(l <= gl && gr <= r)return tr[p];87 Pushdown(p);88 if(l > MID)return Query(l, r, RS, MID + 1, gr);89 if(r < MID + 1)return Query(l, r, LS, gl, MID);90 return Query(l, r, LS, gl, MID) + Query(l, r, RS, MID + 1, gr);91 }92}st;93ll Cal(int R){94 ll ret(0);95 auto vals = st.Query(1, R).vals;96 //r + k >= l + max - min97 for(auto nod : vals)if(R + K >= nod.first)ret += nod.second;98 return ret;99}100
101int mx[MAXN]/*Query Min*/, mn[MAXN]/*Query Max*/;102int mxp(0), mnp(0);103
104int main(){105 N = read(), K = read();106 for(int i = 1; i <= N; ++i)val[i] = read();107 st.Build();108 ll ans(0);109 for(int R = 1; R <= N; ++R){110 while(mxp && val[R] > val[mx[mxp]])st.Modify(mx[mxp - 1] + 1, mx[mxp], val[R] - val[mx[mxp]]), --mxp;111 while(mnp && val[R] < val[mn[mnp]])st.Modify(mn[mnp - 1] + 1, mn[mnp], val[mn[mnp]] - val[R]), --mnp;112 mx[++mxp] = mn[++mnp] = R;113 ans += Cal(R);114 // printf("R = %d, Cal = %lld\n", R, Cal(R));115 }printf("%lld\n", ans);116 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);117 return 0;118}119
120template < typename T >121inline T read(void){122 T ret(0);123 int flag(1);124 char c = getchar();125 while(c != '-' && !isdigit(c))c = getchar();126 if(c == '-')flag = -1, c = getchar();127 while(isdigit(c)){128 ret *= 10;129 ret += int(c - '0');130 c = getchar();131 }132 ret *= flag;133 return ret;134}不过这个东西我们简单分析以下复杂度就会发现,每次合并和修改之后的 Pushup 都会使其重构然后耗费大量时间,所以最后复杂度是
然后对于 basic_string < pair < int, int > > 还有个很严重的问题,对于一般的 C++14 及以下都不会有任何问题,但是在 C++17 之后,因为 basic_string.h 中有如下语段:
xxxxxxxxxx31然而引入的这个头文件中还存在如下语句:
xxxxxxxxxx11static_assert(is_trivial_v<_CharT> && is_standard_layout_v<_CharT>);此时我们发现,这东西会 CE!测试后发现如下语段会输出
xxxxxxxxxx11cout << is_trivial < pair< int, int > >::value << endl;众所周知 is_trivial 一般就是用于判断类型的构造函数是否为默认构造函数,而 pair 的构造函数似乎是用初始化列表写的,可能是因为这个原因,就会导致其无法通过这个 assert,于是就寄了。然而 AT 上默认的不知道是 C++17 还是 20 或者更高,所以无法过编。这个或许可以通过一些高妙的方式解决,但是我不会,于是考虑自定义一个结构体实现跟 pair 一样但是使用默认构造函数即可。
所以话说回来,这个做法本身就是错误的,于是现在我们考虑正解:
思考什么东西比较好维护区间最值和区间等于 我不太喜欢分块这个复杂度不够优秀,所以这里就不给代码实现了,我们考虑一些更优秀的做法。
考虑分治,思路来自机房大佬 @sssmzy,发现对于每一个区间,如果我们令
具体地,对于维护答案的过程,我们发现最大值和最小值的位置无法确定,所以考虑枚举最大值在左侧或右侧,以左侧为例子,我们按照类似猫树的思想,从
当前区间算完之后二分下去分别求解即可,这样最终复杂度
xxxxxxxxxx871
4
11using namespace std;12
13mt19937 rnd(random_device{}());14int rndd(int l, int r){return rnd() % (r - l + 1) + l;}15bool rnddd(int x){return rndd(1, 100) <= x;}16
17typedef unsigned int uint;18typedef unsigned long long unll;19typedef long long ll;20typedef long double ld;21
22
24template < typename T = int >25inline T read(void);26
27int N, K;28int a[MAXN];29ll ans(0);30int mx[MAXN], mn[MAXN];31int buc[MAXN << 1];32
33void Divide(int gl = 1, int gr = N){34 if(gl == gr)return ++ans, void();35 int MID = (gl + gr) >> 1;36 mx[MID] = mn[MID] = a[MID], mx[MID + 1] = mn[MID + 1] = a[MID + 1];37 for(int i = MID - 1; i >= gl; --i)mx[i] = max(mx[i + 1], a[i]), mn[i] = min(mn[i + 1], a[i]);38 for(int i = MID + 2; i <= gr; ++i)mx[i] = max(mx[i - 1], a[i]), mn[i] = min(mn[i - 1], a[i]);39 int sp1(MID), sp2(MID);40 for(int l = MID; l >= gl; --l){41 while(sp1 + 1 <= gr && mx[sp1 + 1] <= mx[l])++sp1, buc[sp1 + mn[sp1]]++;42 while(sp2 + 1 <= gr && mn[sp2 + 1] >= mn[l])++sp2, buc[sp2 + mn[sp2]]--;43 for(int k = 0; k <= K; ++k){44 int r = l + mx[l] - mn[l] - k;45 int idx = l + mx[l] - k;46 if(MID + 1 <= r && r <= min(sp1, sp2))++ans;47 if(sp2 < sp1 && idx > 0)ans += buc[idx];48 }49 }for(int i = MID + 1; i <= gr; ++i)buc[i + mn[i]] = 0;50 sp1 = MID + 1, sp2 = MID + 1;51 for(int r = MID + 1; r <= gr; ++r){52 while(sp1 - 1 >= gl && mx[sp1 - 1] <= mx[r])--sp1, buc[sp1 - mn[sp1] + N]++;53 while(sp2 - 1 >= gl && mn[sp2 - 1] >= mn[r])--sp2, buc[sp2 - mn[sp2] + N]--;54 for(int k = 0; k <= K; ++k){55 int l = r - mx[r] + mn[r] + k;56 int idx = r - mx[r] + k + N;57 if(max(sp1, sp2) <= l && l <= MID)++ans;58 if(sp1 < sp2 && idx > 0)ans += buc[idx];59 }60 }for(int i = gl; i <= MID; ++i)buc[i - mn[i] + N] = 0;61 Divide(gl, MID), Divide(MID + 1, gr);62}63
64int main(){65 N = read(), K = read();66 for(int i = 1; i <= N; ++i)a[i] = read();67 Divide();68 printf("%lld\n", ans);69 fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);70 return 0;71}72
73template < typename T >74inline T read(void){75 T ret(0);76 int flag(1);77 char c = getchar();78 while(c != '-' && !isdigit(c))c = getchar();79 if(c == '-')flag = -1, c = getchar();80 while(isdigit(c)){81 ret *= 10;82 ret += int(c - '0');83 c = getchar();84 }85 ret *= flag;86 return ret;87}UPD
update-2022_11_22 初稿